%f0%9f%94%b4mathsclic Exercice Calcul Dune Fonction Reciproque %f0%9d%91%a5 %e2%86%a6 %f0%9d%91%a5 1 %f0%9d%91%a52

Exercice Mathématique Fonction Réciproque علوم تجريبية موقع قراية En étudiant la fonction f, démontrer que f réalise une bijection de [1, ∞[ sur un intervalle que l'on précisera. retrouver le résultat de la première question et donner une expression explicite de f − 1 en résolvant l'équation y = f(x) d'inconnue x ∈ [1, ∞[. 👉★erratum : f : ] 1;1 [ → ℝ👉★exercice d'analyse sur la détermination d'une fonction réciproque 👉★Énoncé de l'exercice : montrer que l′ application f : ].

Pdf Fonction Réciproque D Une Fonction Continue Fonction Reciproque D Outil pour calculer la réciproque d'une fonction f, c'est à dire la fonction inverse f 1 qui appliquée à la première renvoie la valeur initiale x. Quelles sont celles dont la réciproque est une fonction ? lorsque la réciproque est une fonction, détermine son domaine de définition et son expression analytique. Varier la valeur de « a » à la case #3 ci bas. cliquer sur les points rouge et noir (sur le graphique) pour comparer leur coordonnées (ils sont intervertis). modifier l'équation « f (x)= » à la case #2 pour expérimenter avec différentes fonctions et leurs réciproques respectives. Exercice 13 : [corrigé] montrer que l’application : f : c → c définie par : f(z) = z 2z est bijective et expliciter son application réciproque.

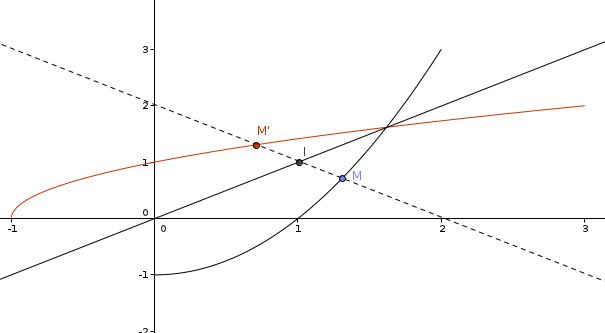
Fonction Reciproque Exercice De Mathématiques De Terminale 485373 Varier la valeur de « a » à la case #3 ci bas. cliquer sur les points rouge et noir (sur le graphique) pour comparer leur coordonnées (ils sont intervertis). modifier l'équation « f (x)= » à la case #2 pour expérimenter avec différentes fonctions et leurs réciproques respectives. Exercice 13 : [corrigé] montrer que l’application : f : c → c définie par : f(z) = z 2z est bijective et expliciter son application réciproque. Fonction réciproque résumé de cours 2, dérivation et étude des fonctions, mathématiques 2ème bac sciences et technologies mécaniques biof, alloschool. Précise si elles sont injectives et donne, le cas échéant, leur fonction réciproque. dans le cas contraire, restreins le domaine de ces fonctions de manière à obtenir une fonction injective et détermine alors également la fonction réciproque. Les enseignants utilisent nos feuilles de calcul pour évaluer la maîtrise des faits mathématiques de base par les élèves, pour leur donner des exercices supplémentaires, pour leur enseigner de nouvelles stratégies mathématiques et pour gagner un temps précieux de planification. On obtient finalement le dl suivant pour la fonction $f^ { 1}$ : $$f^ { 1} (y)=y y^3 o (y^4).$$ on aurait pu, pour simplifier un peu les calculs, remarquer que la fonction $f^ { 1}$, tout comme la fonction $f$, est impaire, et donc que les coefficients d'ordre pair du dl sont nuls.

Fonction Réciproque D Une Fonction Strictement Monotone Sur Un Fonction réciproque résumé de cours 2, dérivation et étude des fonctions, mathématiques 2ème bac sciences et technologies mécaniques biof, alloschool. Précise si elles sont injectives et donne, le cas échéant, leur fonction réciproque. dans le cas contraire, restreins le domaine de ces fonctions de manière à obtenir une fonction injective et détermine alors également la fonction réciproque. Les enseignants utilisent nos feuilles de calcul pour évaluer la maîtrise des faits mathématiques de base par les élèves, pour leur donner des exercices supplémentaires, pour leur enseigner de nouvelles stratégies mathématiques et pour gagner un temps précieux de planification. On obtient finalement le dl suivant pour la fonction $f^ { 1}$ : $$f^ { 1} (y)=y y^3 o (y^4).$$ on aurait pu, pour simplifier un peu les calculs, remarquer que la fonction $f^ { 1}$, tout comme la fonction $f$, est impaire, et donc que les coefficients d'ordre pair du dl sont nuls.

Fonction Logarithme I Fonction Reciproque 1â La Les enseignants utilisent nos feuilles de calcul pour évaluer la maîtrise des faits mathématiques de base par les élèves, pour leur donner des exercices supplémentaires, pour leur enseigner de nouvelles stratégies mathématiques et pour gagner un temps précieux de planification. On obtient finalement le dl suivant pour la fonction $f^ { 1}$ : $$f^ { 1} (y)=y y^3 o (y^4).$$ on aurait pu, pour simplifier un peu les calculs, remarquer que la fonction $f^ { 1}$, tout comme la fonction $f$, est impaire, et donc que les coefficients d'ordre pair du dl sont nuls.