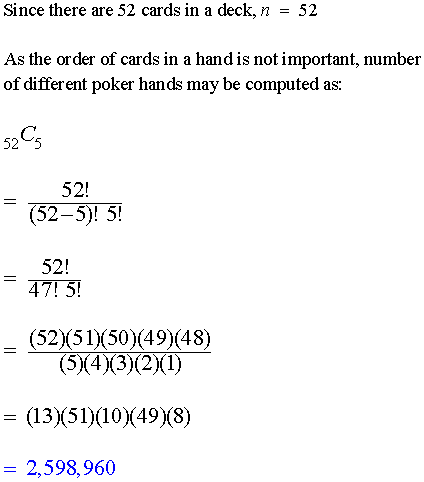
Combinations Probability Statistics Help Combinations are a fundamental concept in mathematics, and they arise in numerous everyday situations. a combination is a selection of items from a larger set, where the order of selection does not matter. in this article, we will discuss into 10 examples of combinations in math. Combinations. there are also two types of combinations (remember the order does not matter now): repetition is allowed: such as coins in your pocket (5,5,5,10,10) no repetition: such as lottery numbers (2,14,15,27,30,33) 1. combinations with repetition. actually, these are the hardest to explain, so we will come back to this later. 2.

10 Examples Of Combinations In Math Here, we will look at a brief summary of combinations along with their formula and the terminology used. in addition, we will see examples with answers to learn about the application of the combination formula. In mathematics, a combination is a way of selecting items from a collection where the order of selection does not matter. suppose we have a set of three numbers p, q and r. then in how many ways we can select two numbers from each set, is defined by combination. We have jotted down some interesting examples in this write up to help you understand how these math concepts find their way into the real world. so, keep reading! 1. combination lock. a combination lock is a useful item that helps safeguard our belongings when we are out and about. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. after reading this article, you should understand: combination formula and its derivation; difference between permutation and combination; how to solve problems related to.

Combinations We have jotted down some interesting examples in this write up to help you understand how these math concepts find their way into the real world. so, keep reading! 1. combination lock. a combination lock is a useful item that helps safeguard our belongings when we are out and about. Combinations refer to the possible arrangements of a set of given objects when changing the order of selection of the objects is not treated as a distinct arrangement. after reading this article, you should understand: combination formula and its derivation; difference between permutation and combination; how to solve problems related to. Let us learn more about how to calculate combinations, combinations formula, differences between permutation and combinations, with the help of examples, faqs. what are combinations? combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combination is a way of choosing items from a set, (unlike permutations) when the order of selection doesn’t matter. in smaller cases, it’s possible to count the number of combinations. combination refers to the mixture of n things taken k at a time without repetition. In mathematics, a combination is the number of possible arrangements of objects or elements from a group when the order of selection doesn’t matter. in other words, combinations show us how many different possible subsets we can form from the larger set. for instance, suppose you are going on a five day vacation where the planned activities are:. Combinations are a cornerstone of combinatorics, focusing on the number of ways to select items from a set where the order of selection does not matter. unlike permutations, where the sequence defines distinct outcomes, combinations treat selections as identical regardless of arrangement.

Revision Exercise On Permutations And Combinations Combination Math Let us learn more about how to calculate combinations, combinations formula, differences between permutation and combinations, with the help of examples, faqs. what are combinations? combinations are selections made by taking some or all of a number of objects, irrespective of their arrangements. Combination is a way of choosing items from a set, (unlike permutations) when the order of selection doesn’t matter. in smaller cases, it’s possible to count the number of combinations. combination refers to the mixture of n things taken k at a time without repetition. In mathematics, a combination is the number of possible arrangements of objects or elements from a group when the order of selection doesn’t matter. in other words, combinations show us how many different possible subsets we can form from the larger set. for instance, suppose you are going on a five day vacation where the planned activities are:. Combinations are a cornerstone of combinatorics, focusing on the number of ways to select items from a set where the order of selection does not matter. unlike permutations, where the sequence defines distinct outcomes, combinations treat selections as identical regardless of arrangement.

Matematickcom On Tumblr In mathematics, a combination is the number of possible arrangements of objects or elements from a group when the order of selection doesn’t matter. in other words, combinations show us how many different possible subsets we can form from the larger set. for instance, suppose you are going on a five day vacation where the planned activities are:. Combinations are a cornerstone of combinatorics, focusing on the number of ways to select items from a set where the order of selection does not matter. unlike permutations, where the sequence defines distinct outcomes, combinations treat selections as identical regardless of arrangement.
