
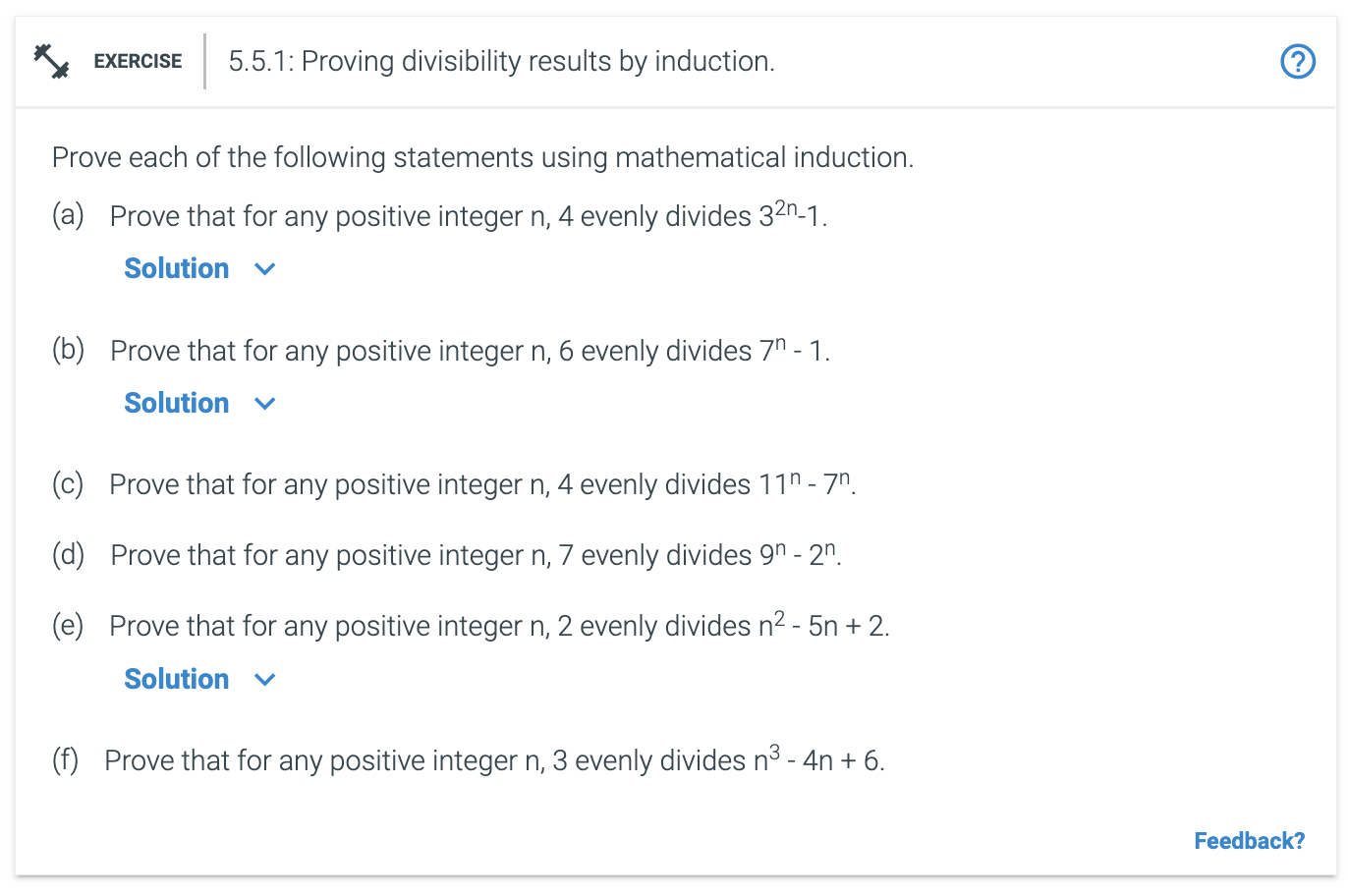
Solved Prove Each Of The Following Statements Using Chegg Prove the following statement using mathematical induction. n! > 2 n for n ≥ 4 [note: this is a very important result and you should remember it] base case: general case which should include the following steps: (i) first, clearly state inductive hypothesis: (ii) then clearly indicate what should be proved: (iii) finally, show the actual. Prove the following problem using mathematical induction. can greatly help see the steps needed in this proof. ( the n^n means. n raised to the power of n.) provide the format in accordance to the blanks if possible. there’s just one step to solve this. n ≠ 2 ≠ 2 and n n = 2 2 = 4. so, n!
Solved Prove Each Of The Following Statements Using Chegg Exercise 6.4.2: proving identities by induction. prove each of the following statements using mathematical induction. Prove the following using mathematical induction, for n∈z ∑k=1n2k=n2 n. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Math; advanced math; advanced math questions and answers; use the " n 1 to n " form of mathematical induction to prove each of the following.a) 12 14 18 cdots 12n=1 12n for all n≥1.b) n3 2n is a multiple 3 for all n≥1.c) in calculus you learned several derivative rules, including [sin(x)]'=cos(x) and [ln(x)]'=1x. 1.^ these offers are provided at no cost to subscribers of chegg study and chegg study pack. no cash value. terms and conditions apply. please visit each partner activation page for complete details. 2.^ chegg survey fielded between sept. 9–oct 3, 2024 among a random sample of u.s. customers who used chegg study or chegg study pack in q2 2024 and q3 2024.
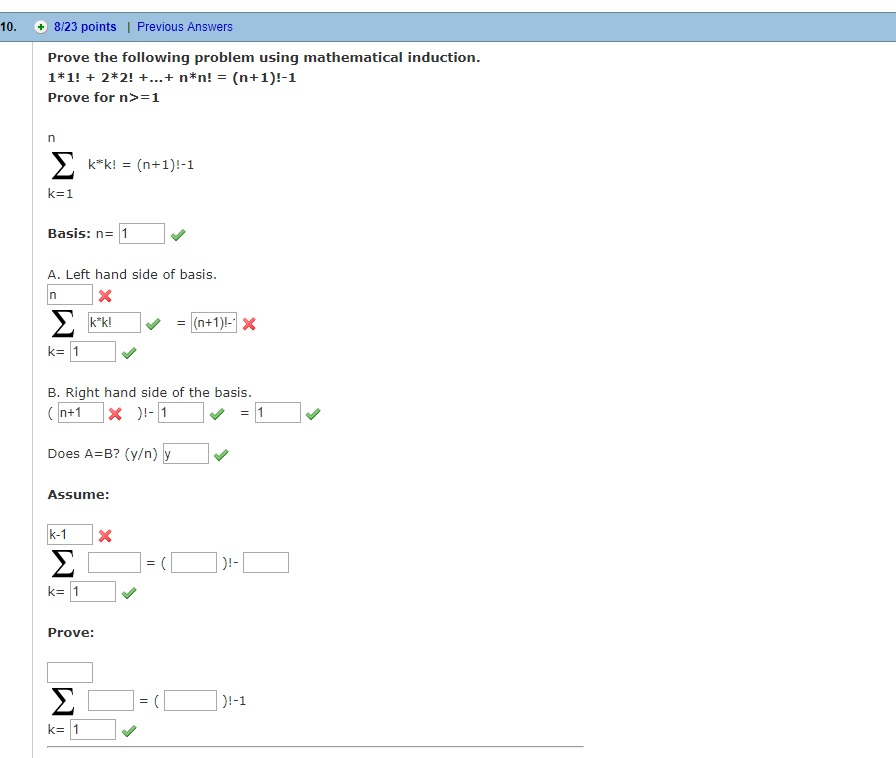
Solved Prove The Following Problem Using Chegg Math; advanced math; advanced math questions and answers; use the " n 1 to n " form of mathematical induction to prove each of the following.a) 12 14 18 cdots 12n=1 12n for all n≥1.b) n3 2n is a multiple 3 for all n≥1.c) in calculus you learned several derivative rules, including [sin(x)]'=cos(x) and [ln(x)]'=1x. 1.^ these offers are provided at no cost to subscribers of chegg study and chegg study pack. no cash value. terms and conditions apply. please visit each partner activation page for complete details. 2.^ chegg survey fielded between sept. 9–oct 3, 2024 among a random sample of u.s. customers who used chegg study or chegg study pack in q2 2024 and q3 2024. In order to prove a mathematical statement involving integers, we may use the following template: suppose \(p(n), \forall n \geq n 0, \, n, \, n 0 \in \mathbb{z }\) be a statement. for regular induction:. 2 = n(n 1)(n 2) 6 proof: for n = 1, the statement reduces to 1 = 1 2 3 6 and is obviously true. assuming the statement is true for n = k: 1 3 6 10 k(k 1) 2 = k(k 1)(k 2) 6; (7) we will prove that the statement must be true for n = k 1: 1 3 6 10 (k 1)(k 2) 2 = (k 1)(k 2)(k 3) 6: (8) the left hand side of. 2 n 1 ≤ n ! there are 3 steps to solve this one. mathematical induction is a technique of proving a statement, theorem or formula which is thought to not the question you’re looking for? post any question and get expert help quickly. answer to prove the following by using mathematical induction. In this section, we deal with how theorems are proven and how mathematicians decide what statements they should try to prove. analogy and induction are useful in discovering theorems. but when it comes to proofs, analogy and induction are inadequate. it is the view of modern mathematics that proofs must be deductive.
