Mit Integration Bee Mit integration bee: finals (time limit per integral: 4 minutes) finals problem 1 z finals problem 3 z1 2 finals problem 5 z1 0 ∞ ∑ n=1 ⌊2nx⌋ 3n!2 dx = 27 32. created date: 1 23 2023 10:07:26 pm. The integrals and answers can be found at math.mit.edu ~yyao1 pdf 2023 finals.pdfplaylist for the full event: playlist?list=p.

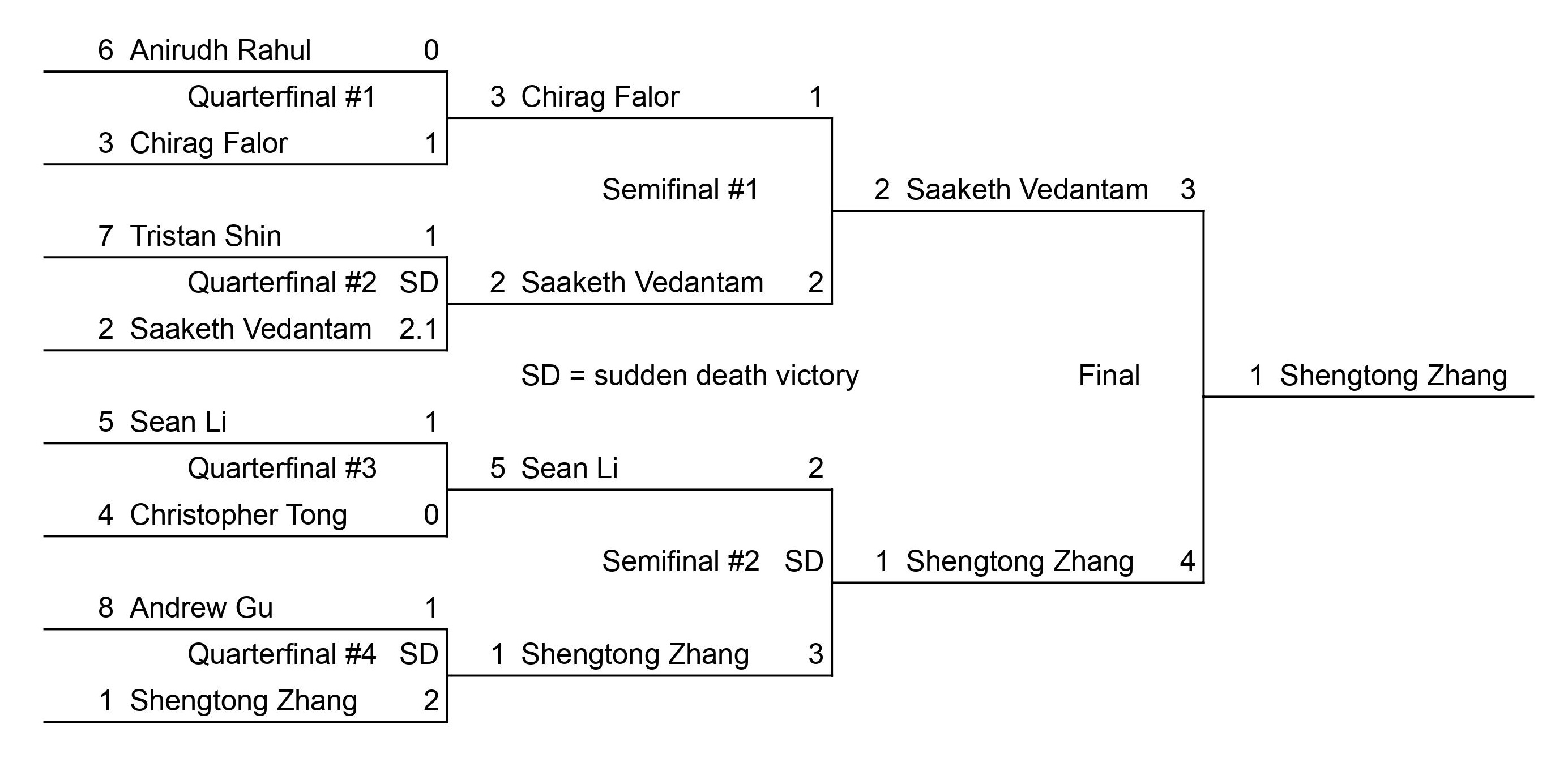
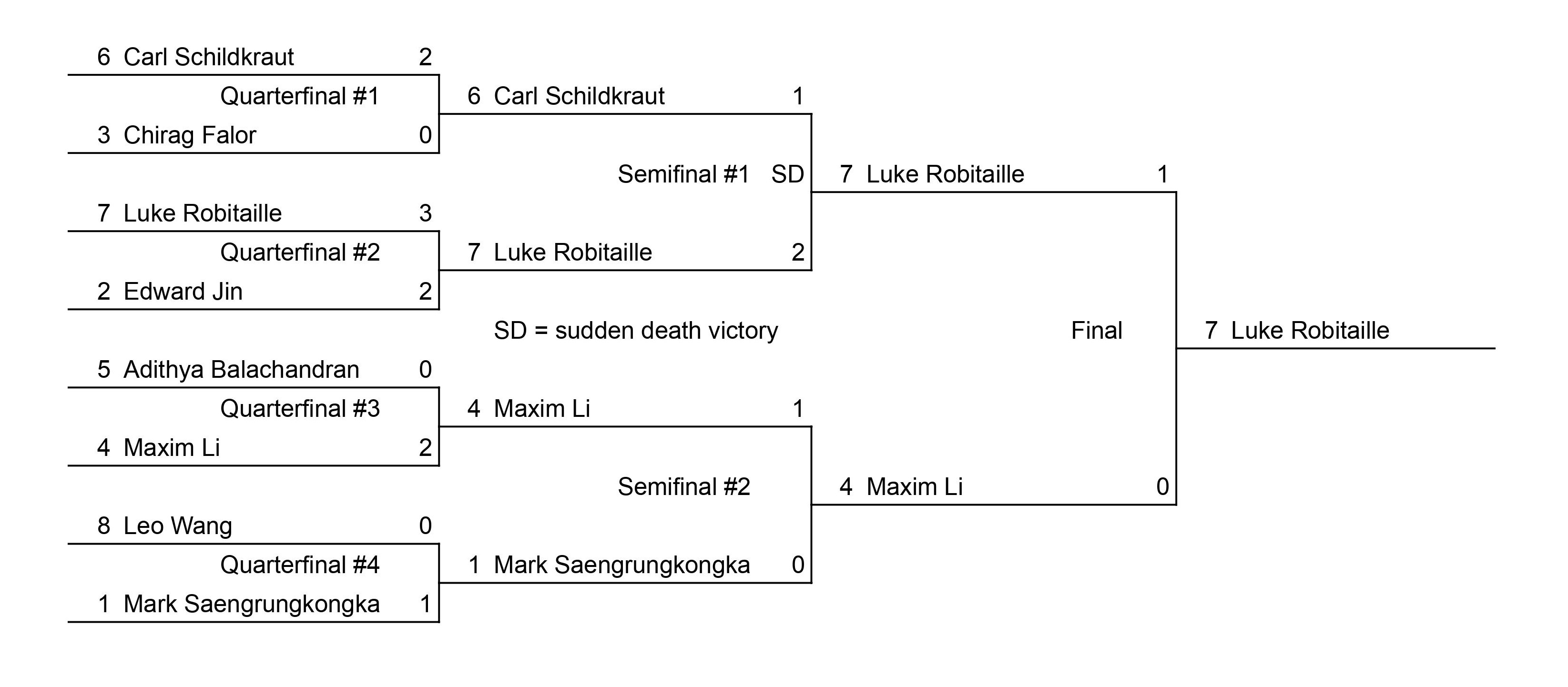
Mit Integration Bee 2023 рџђќ I Can You Solve This Explained R 2023 results. the 42nd annual integration bee took place on thursday, january 26th, 2023. eight students advanced to the playoff bracket: the top four students in 2023 were (pictured below with some of their prizes): luke robitaille (grand integrator) maxim li; mark saengrungkongka; carl schildkraut. Sit back, relax and enjoy the wild ride of evaluating the beastly integrals from the 2023 finals.thank you myers for the wonderful solution development for p. I would like to solve the first problem of the 2023 mit integration bee finals, which is the following integral : $$\int 0^{\pi 2} \frac{\sqrt[3]{\tan x}}{(\cos x \sin x)^2}dx$$ i tried substitut. This book contains the solutions with some details to all the questions of the mit integration bee, which were asked in qualifying, regular, quarterfinal, semifinal, and final tests in 2023.

2023 Mit Integration Bee рџђќ Integral Calculus With Nested Fractions I would like to solve the first problem of the 2023 mit integration bee finals, which is the following integral : $$\int 0^{\pi 2} \frac{\sqrt[3]{\tan x}}{(\cos x \sin x)^2}dx$$ i tried substitut. This book contains the solutions with some details to all the questions of the mit integration bee, which were asked in qualifying, regular, quarterfinal, semifinal, and final tests in 2023. Mit integration bee: 2023 final question 1 ∫ 2 0 3 √ tan (sin cos )2 d (1.1) solution with the change of variable = 3 √ tan , we have = 3 √ tan , 3 2d = sec2 d . (1.2) therefore, the integral becomes = ∫ 2 0 3 √ tan (sin cos )2 d = ∫ ∞ 0 3 3 d (sin cos )2 sec2 = ∫ ∞ 0 3 3 d ( 3 1)2 = − 3 1 ∞ 0. I was watching the 2023 mit integration bee on , and for fun, i tried to evaluate the final problem myself, which is the following definite integral: $$\int 0^1\left(\sum {n=1}^\infty \frac{\. 2023 02 03 topics calculus, integration, mit collection opensource item size 696.3k. Mit integration bee is a yearly tradition every january in mit. i do it just for fun and, of course, i don’t have the time limit :). my solutions are posted below. fairly speaking, i also grabbed the hints from others for some problems, and sometimes the techniques are pretty amazing.

Mit Integration Bee Finals Problem 2 By Complexbulb Medium Mit integration bee: 2023 final question 1 ∫ 2 0 3 √ tan (sin cos )2 d (1.1) solution with the change of variable = 3 √ tan , we have = 3 √ tan , 3 2d = sec2 d . (1.2) therefore, the integral becomes = ∫ 2 0 3 √ tan (sin cos )2 d = ∫ ∞ 0 3 3 d (sin cos )2 sec2 = ∫ ∞ 0 3 3 d ( 3 1)2 = − 3 1 ∞ 0. I was watching the 2023 mit integration bee on , and for fun, i tried to evaluate the final problem myself, which is the following definite integral: $$\int 0^1\left(\sum {n=1}^\infty \frac{\. 2023 02 03 topics calculus, integration, mit collection opensource item size 696.3k. Mit integration bee is a yearly tradition every january in mit. i do it just for fun and, of course, i don’t have the time limit :). my solutions are posted below. fairly speaking, i also grabbed the hints from others for some problems, and sometimes the techniques are pretty amazing.

Pdf Mit Integration Bee 2023 Solutions Of Qualifying Regular 2023 02 03 topics calculus, integration, mit collection opensource item size 696.3k. Mit integration bee is a yearly tradition every january in mit. i do it just for fun and, of course, i don’t have the time limit :). my solutions are posted below. fairly speaking, i also grabbed the hints from others for some problems, and sometimes the techniques are pretty amazing.
Mit Integration Bee Informacionpublica Svet Gob Gt
