3 2 Derivate Formulas P3 Calculus I Definition Of Derivative Rimma

3 1 3 2 The Derivative Pdf Tangent Derivative Defines derivatives by using power rule and limits calculus definition of derivative rimma feygelson important: the quotient rule for derivative example 22. In this text we use both forms of the definition. as before, the choice of definition will depend on the setting. now that we have formally defined a tangent line to a function at a point, we can use this definition to find equations of tangent lines.

Derivative Formulas A Comprehensive Guide To Calculus Course Hero The definition of the derivative – in this section we define the derivative, give various notations for the derivative and work a few problems illustrating how to use the definition of the derivative to actually compute the derivative of a function. Now that we have both a conceptual understanding of a limit and the practical ability to compute limits, we have established the foundation for our study of calculus, the branch of mathematics in which we compute derivatives and integrals. We’re now going to formalize this into the definition of “one of the two central concepts of calculus: the derivative.”. For the following exercises, use the limit definition of derivative to show that the derivative does not exist at [latex]x=a [ latex] for each of the given functions.
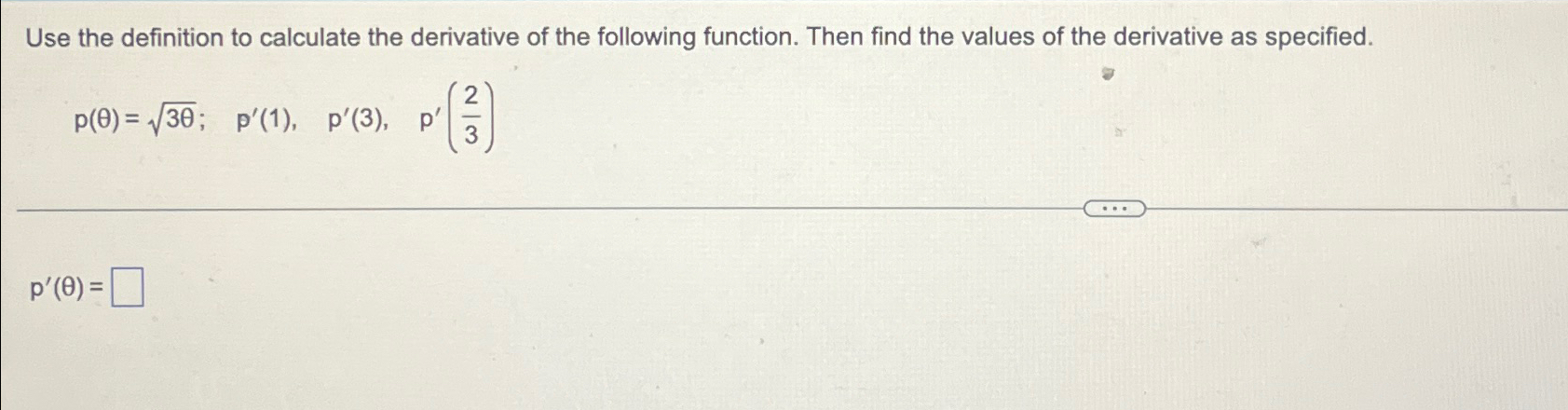
Solved Use The Definition To Calculate The Derivative Of The Chegg We’re now going to formalize this into the definition of “one of the two central concepts of calculus: the derivative.”. For the following exercises, use the limit definition of derivative to show that the derivative does not exist at [latex]x=a [ latex] for each of the given functions. The derivative of position as a function of time is velocity, or the (time) rate of change of position. likewise the derivative of a function is the rate of change of the value of the function value with respect to change in the value of its argument. It would be labor intensive (and impossible) to use the definition above to find the (first) derivative of a given function for every one of the infinite points in its domain. This is because the derivative measures the rate of change of a function with respect to a variable, and since constants, by definition, do not change, their derivative is hence zero. In this section we give most of the general derivative formulas and properties used when taking the derivative of a function. examples in this section concentrate mostly on polynomials, roots and more generally variables raised to powers.

Calculus Ii 1 The Derivative 1 The Derivative This Chapter Gives A The derivative of position as a function of time is velocity, or the (time) rate of change of position. likewise the derivative of a function is the rate of change of the value of the function value with respect to change in the value of its argument. It would be labor intensive (and impossible) to use the definition above to find the (first) derivative of a given function for every one of the infinite points in its domain. This is because the derivative measures the rate of change of a function with respect to a variable, and since constants, by definition, do not change, their derivative is hence zero. In this section we give most of the general derivative formulas and properties used when taking the derivative of a function. examples in this section concentrate mostly on polynomials, roots and more generally variables raised to powers.

Calculus 2 Pdf Derivative Equations This is because the derivative measures the rate of change of a function with respect to a variable, and since constants, by definition, do not change, their derivative is hence zero. In this section we give most of the general derivative formulas and properties used when taking the derivative of a function. examples in this section concentrate mostly on polynomials, roots and more generally variables raised to powers.

Calculus 1 Chapter 3 Derivatives Part 5 Implicit Differentiation
Comments are closed.