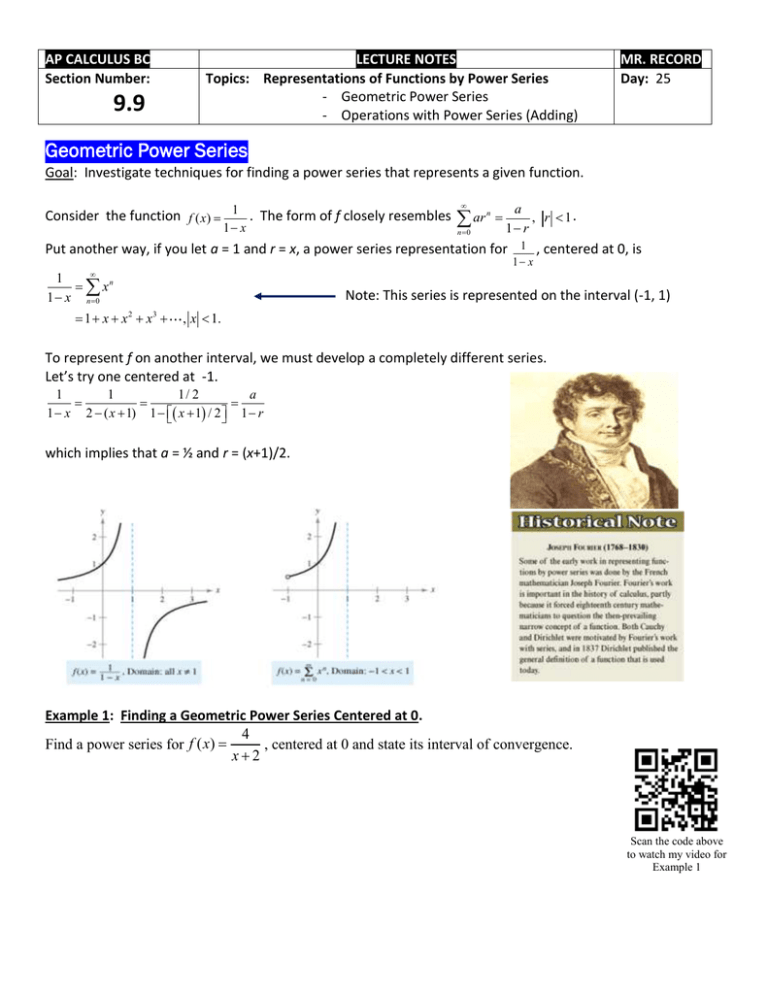
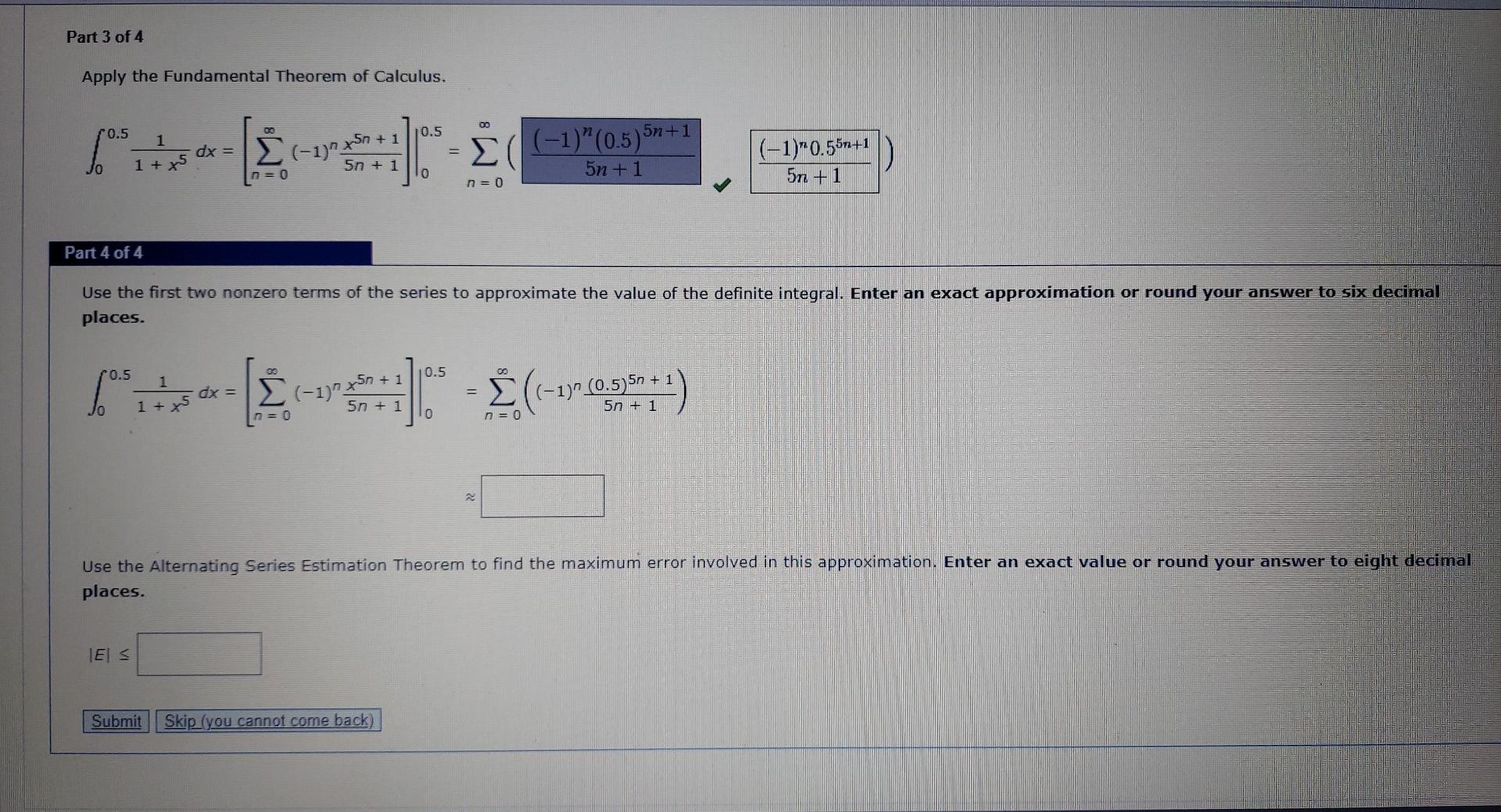
9 9 Representations Of Functions By Power Series Power series representations of functions can be systematically derived by manipulating the geo metric series formula. the process involves the following steps: this is a foundational representation for f(x) = , valid on the interval ( 1; 1). the series for related functions. rive series for functions such as ln(1 x), tan 1 x, or similar. Use a power series to represent each of the following functions f f. find the interval of convergence. this function is not in the exact form of a sum of a geometric series. however, with a little algebraic manipulation, we can relate to a geometric series. by factoring 4 out of the two terms in the denominator, we obtain.

Solved 17 Question From 11 9 Representations Of Functions Chegg 本节将研究如何对特定类型的函数通过对 几何级数 代数变形或进行微分或积分运算以表示成 幂级数 的形式. 转化为幂级数表示常用于非基本初等函数的反导数,解微分方程以及对函数的多项式近似表示. 从 11.2节例题 6. 可知 \frac {1} {1 x}=1 x x^2 x^3 …=\sum {n=0}^ {\infty} {x^n} ( \left| x \right|<1 ). 此即由 a=1 , r=x 时的几何级数得到的幂级数表示. 注意此时应将上述方程视为对函数 f\left ( x \right)=\frac {1} {1 x} 表示为幂级数之和. 更多示例参见下述例题 1. ~ 3. In this section we learn how to represent certain types of functions as sums of power series by manipulating geometric series or by differentiating or integrating such a series. we learned the geometric series. Math 1132 worksheet 11.9 name: discussion section: 11.9 representations of functions as power series power series, derivatives, and integrals. if the power series x1 n=0 c n(xa)n has a radius of convergence r>0, then the function f defined by f(x)=c 0 c 1(x a) c 2(x a)2 ···= x1 n=0 c n(x a)n. Now we know that some functions can be expressed as power series, which look like infinite polynomials. since calculus, that is, computation of derivatives and antiderivatives, is easy for polynomials, the obvious question is whether the same is true for infinite series. the answer is yes: suppose the power series.

Solved Representations Of Functions As Power Series Part 1 Chegg Math 1132 worksheet 11.9 name: discussion section: 11.9 representations of functions as power series power series, derivatives, and integrals. if the power series x1 n=0 c n(xa)n has a radius of convergence r>0, then the function f defined by f(x)=c 0 c 1(x a) c 2(x a)2 ···= x1 n=0 c n(x a)n. Now we know that some functions can be expressed as power series, which look like infinite polynomials. since calculus, that is, computation of derivatives and antiderivatives, is easy for polynomials, the obvious question is whether the same is true for infinite series. the answer is yes: suppose the power series. Power series representations of functions can be systematically derived by manipulating the geo metric series formula. the process involves the following steps: = 1 x x2 x3 · · · = xn, |x| < 1. this is a foundational representation for f(x) = , valid on the interval ( 1, 1). Power series are used to represent common functions and also to define new functions. in this section we define power series and show how to determine when a power series converges and when it diverges. we also show how to represent certain functions using power series. a series of the form. ∞ ∑ n = 0cnxn = c0 c1x c2x2 …,. Section 12.9: representations of functions as power series differentiation and integration of power series: if the domain of a power series (i.e., the interval of convergence) is not a single point, then (with the possible exception of endpoints—see note below): 1. f is differentiable in the same domain: and or note:. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. however, use of this formula does quickly illustrate how functions can be represented as a power series. we also discuss differentiation and integration of power series.
Solved Representations Of Functions As Power Series Part 1 Chegg Power series representations of functions can be systematically derived by manipulating the geo metric series formula. the process involves the following steps: = 1 x x2 x3 · · · = xn, |x| < 1. this is a foundational representation for f(x) = , valid on the interval ( 1, 1). Power series are used to represent common functions and also to define new functions. in this section we define power series and show how to determine when a power series converges and when it diverges. we also show how to represent certain functions using power series. a series of the form. ∞ ∑ n = 0cnxn = c0 c1x c2x2 …,. Section 12.9: representations of functions as power series differentiation and integration of power series: if the domain of a power series (i.e., the interval of convergence) is not a single point, then (with the possible exception of endpoints—see note below): 1. f is differentiable in the same domain: and or note:. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. however, use of this formula does quickly illustrate how functions can be represented as a power series. we also discuss differentiation and integration of power series.

Solved 9 9 9 10 Find Power Series Representations For Each Chegg Section 12.9: representations of functions as power series differentiation and integration of power series: if the domain of a power series (i.e., the interval of convergence) is not a single point, then (with the possible exception of endpoints—see note below): 1. f is differentiable in the same domain: and or note:. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. however, use of this formula does quickly illustrate how functions can be represented as a power series. we also discuss differentiation and integration of power series.
