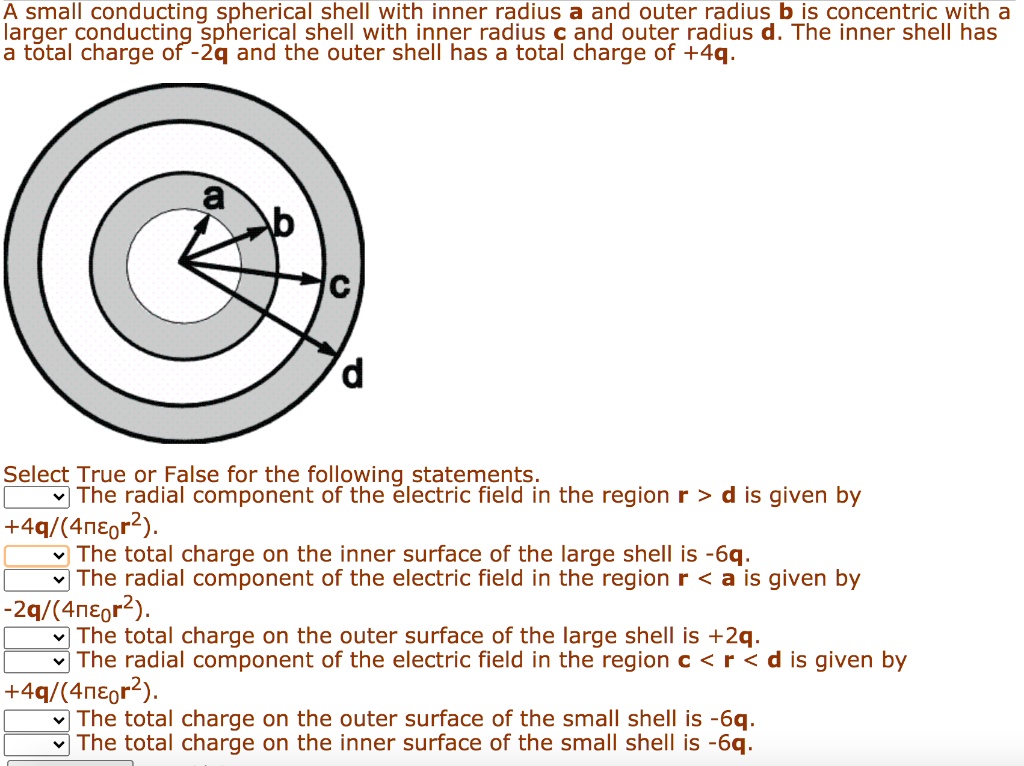
Solved A Small Conducting Spherical Shell With Inner Radius A And (a) charge q resides on outer surface of spherical conducting shell. due to charge q placed at centre, charge induced on inner surface is –q and on outer surface it is q. so, total charge on inner surface q and on outer surface it is q q. surface charge density on inner surface = q 4 π r 12. Question: (25%) problem 2: a conducting spherical shell of inner radius r1 and outer radius r2 has a point charge q fixed at its center. the spherical shell has a net charge of aq. r2 taq 4 33% part (a) enter an expression for the surface charge density on the inner surface of the spherical shell, using the variables provided.
Solved A Solid Conducting Spherical Shell Of Inner Radius R1 And Outer As the shell is spherical in shape, we get the surface area of the inner shell to be 4 π r 1 2 where r 1 is the radius of the inner shell and the charge on the inner shell is − q . so, we can put the value of the charge and surface area of the inner shell into equation (1), we get,. A spherical conducting shell of inner radius r 1 and outer radius r 2 has a charge q. (a) a charge q is placed at the centre of the shell. what is the surface charge density on the inner and outer surfaces of the shell?. As the charge q is placed at the centre of the shell, there is charge –q induced on the inner surface and a charge q is induced on the outer surface of the shell. thus, the total charge on the inner surface of the shell is – q and on the outer surface of the shell is (q q). Question: a point charge q is at the center of a spherical conducting shell of inner radius r1 and outer radius r2, as shown in the figure below. the total charge on the inner surface of the shell is zero o 012 o q o a12. thank you! there are 2 steps to solve this one.
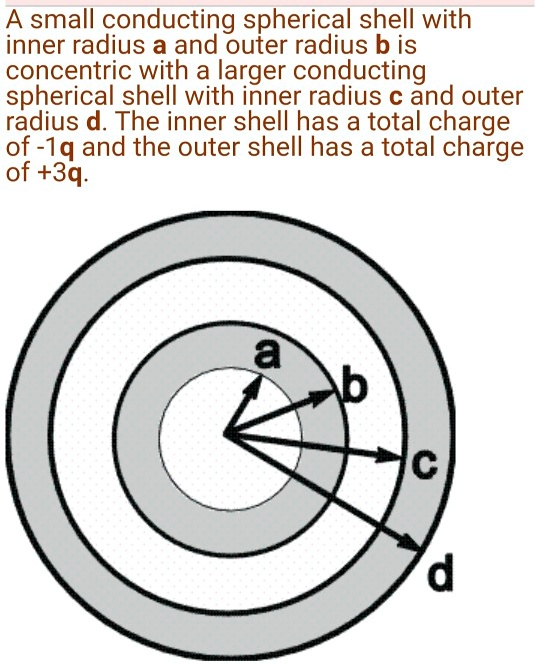
Solved A Small Conducting Shell With Inner Radius A And Outer Radius B As the charge q is placed at the centre of the shell, there is charge –q induced on the inner surface and a charge q is induced on the outer surface of the shell. thus, the total charge on the inner surface of the shell is – q and on the outer surface of the shell is (q q). Question: a point charge q is at the center of a spherical conducting shell of inner radius r1 and outer radius r2, as shown in the figure below. the total charge on the inner surface of the shell is zero o 012 o q o a12. thank you! there are 2 steps to solve this one. It consists of two concentric conducting spherical shells of radii r 1 r 1 (inner shell) and r 2 r 2 (outer shell). the shells are given equal and opposite charges q q and − q − q, respectively. from symmetry, the electrical field between the shells is directed radially outward. A metallic spherical shell has an inner radius r 1 and outer radius r 2. a charge q is placed at the centre of the spherical cavity. what will be surface charge density on (i) the inner surface, and (ii) the outer surface?. A conducting spherical shell of inner radius r 1 and outer radius r 2 has a point charge q at its center. the spherical shell has a net charge of a q. enter an expression for the surface charge density on the inner surface of the spherical shell. The charge of magnitude q present inside the spherical shell induces a charge of magnitude −q.o n the inner part of the shell. therefore, for the charge on the inner part, the surface charge density will be due to −q. it is given by: σ1 =total charge surface area of inner part. ⇒ q 4 π r 1 2.

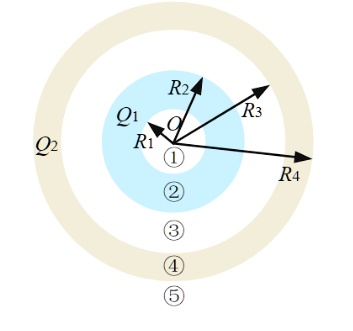
A Solid Conducting Sphere Of Radius Ra Is Placed Concentrically Inside It consists of two concentric conducting spherical shells of radii r 1 r 1 (inner shell) and r 2 r 2 (outer shell). the shells are given equal and opposite charges q q and − q − q, respectively. from symmetry, the electrical field between the shells is directed radially outward. A metallic spherical shell has an inner radius r 1 and outer radius r 2. a charge q is placed at the centre of the spherical cavity. what will be surface charge density on (i) the inner surface, and (ii) the outer surface?. A conducting spherical shell of inner radius r 1 and outer radius r 2 has a point charge q at its center. the spherical shell has a net charge of a q. enter an expression for the surface charge density on the inner surface of the spherical shell. The charge of magnitude q present inside the spherical shell induces a charge of magnitude −q.o n the inner part of the shell. therefore, for the charge on the inner part, the surface charge density will be due to −q. it is given by: σ1 =total charge surface area of inner part. ⇒ q 4 π r 1 2.
