
A Thin Spherical Conducting Shell Of Radius R Has A Charge Q Another A thin spherical conducting shell of radius r has a charge q. another charge q is placed at the centre of the shell. the electrostatic potential at a point p a distance `r 2` from the centre of the shell is. Final answer: the electrostatic potential at point p due to q and q is option b) $v = \dfrac{{2q}}{{4\pi {\varepsilon o}r}} \dfrac{{2q}}{{4\pi {\varepsilon o}r}}$. note: here first find out the electric potential due to q and then electric potential due to q.

A Thin Spherical Conducting Shell Has Radius R And Charge Q Another A thin spherical conducting shell of radius r has a charge q. a point charge q is placed at the centre of the shell. find (i) the charge density on the outer surface of the shell and. For a spherical shell at distance r from the point charge, the integral `ointda` is merely the sum of all differential of da on the sphere. therefore, `oint da =4pir^2` `epsi 0e(4pir^2) = q`. Q. a thin spherical conducting shell of radius r has a charge q. another charge q is placed at the center of the shell. the electric potential at a point p at distance 2 r from the center of the shell is (q = 10 μ c, q = − 2 μ c). A thin conducting spherical shell of radius r has charge q spread uniformly over its surface. using gauss’s law, derive an expression for an electric field at a point outside the shell. draw a graph of electric field e(r) with distance r from the centre of the shell or 0 ≤ r ≤ ∞.
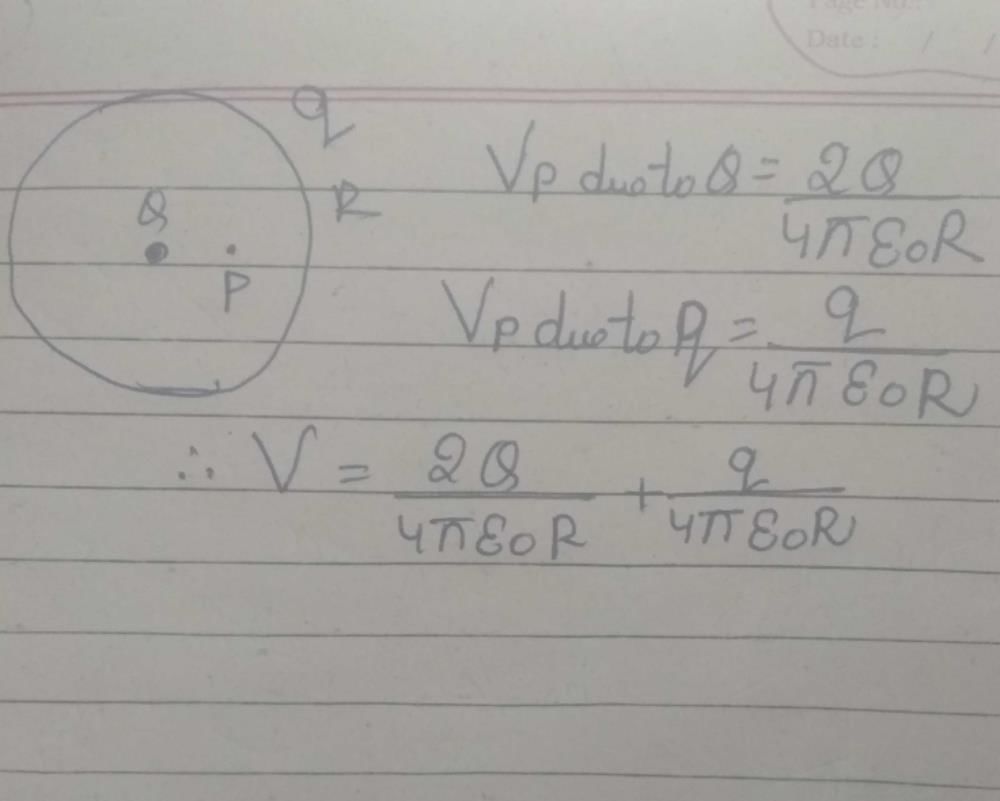
A Thin Spherical Conducting Shell Of Radius R Has Charge Q Another Q. a thin spherical conducting shell of radius r has a charge q. another charge q is placed at the center of the shell. the electric potential at a point p at distance 2 r from the center of the shell is (q = 10 μ c, q = − 2 μ c). A thin conducting spherical shell of radius r has charge q spread uniformly over its surface. using gauss’s law, derive an expression for an electric field at a point outside the shell. draw a graph of electric field e(r) with distance r from the centre of the shell or 0 ≤ r ≤ ∞. Step 1: find the potential at the surface of the conducting shell. where r is the distance of the point from the center of the shell. the total potential at point p is the sum of the potentials due to q and q. so, hence, the electrostatic potential at point p is 2q 4πε₀r q 4πε₀r = 2q 4πε₀r q 4πε₀r. the correct option is d. The potential at point p is only due to the charge q at the center of the shell. the formula to calculate the potential at a point due to a point charge is v = k * q r, where v is the potential, k is the electrostatic constant, q is the charge, and r is the distance from the charge. in this case, the distance from the charge q to point p is r. A thin spherical conducting shell of radius r has a charge q. another charge q is placed at the centre of the shell. the electrostatic potential at a point p a distance 2 r from the centre of the shell is. A small conducting sphere of radius 'r' carrying a charge q is surrounded by a large concentric conducting shell of radius ron which a charge q is placed. using gauss's law, derive the expressions for the electric field at a point 'x' (i) between the sphere and the shell (r < x < r), (ii) outside the spherical shell.

Answered 43 A Thin Spherical Conducting Shell Of Radius R Has A Kunduz Step 1: find the potential at the surface of the conducting shell. where r is the distance of the point from the center of the shell. the total potential at point p is the sum of the potentials due to q and q. so, hence, the electrostatic potential at point p is 2q 4πε₀r q 4πε₀r = 2q 4πε₀r q 4πε₀r. the correct option is d. The potential at point p is only due to the charge q at the center of the shell. the formula to calculate the potential at a point due to a point charge is v = k * q r, where v is the potential, k is the electrostatic constant, q is the charge, and r is the distance from the charge. in this case, the distance from the charge q to point p is r. A thin spherical conducting shell of radius r has a charge q. another charge q is placed at the centre of the shell. the electrostatic potential at a point p a distance 2 r from the centre of the shell is. A small conducting sphere of radius 'r' carrying a charge q is surrounded by a large concentric conducting shell of radius ron which a charge q is placed. using gauss's law, derive the expressions for the electric field at a point 'x' (i) between the sphere and the shell (r < x < r), (ii) outside the spherical shell.
