
Mths221 Note 18 The Ratio Test Root Test And Absolute And Theroem 11.7.3: the root test. suppose that \[\lim {n\to \infty} |a n|^{1 n}=l. \nonumber \] if \(l < 1\),the series \(\sum a n\) converges absolutely, if \(l>1\) the series diverges, and if \(l=1\) this test gives no information. Annette pilkington lecture 28 :absolute convergence, ratio and root test absolute conv. implies conv. theorem if a series is absolutely convergent, then it is convergent, that is.
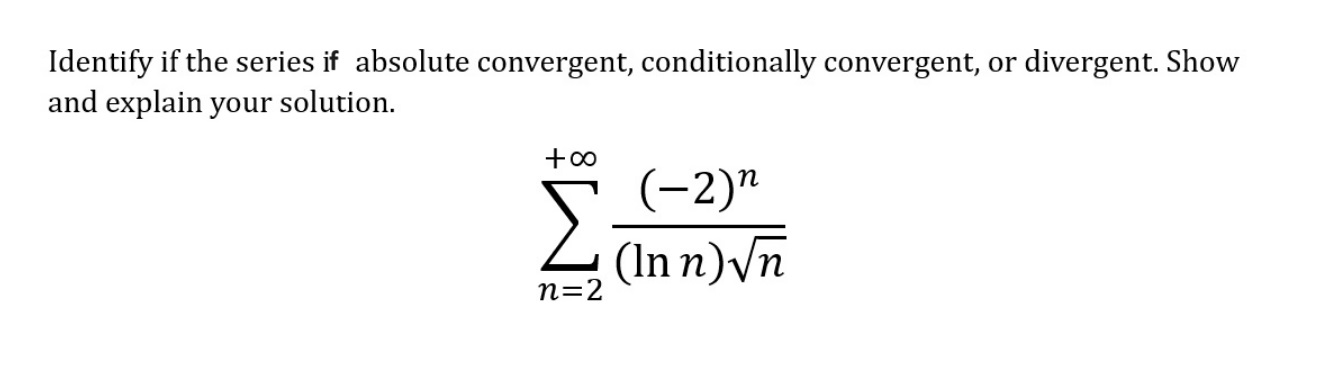
Solved Please Try To Use Absolute Convergence Ratio Test Chegg The ratio test this test is useful for determining absolute convergence. let p 1 n=1 a n be a series (the terms may be positive or negative). let l = lim n!1 a n 1 an . if l < 1, then the series p 1 n=1 a n converges absolutely (and hence is convergent). if l > 1 or 1, then the series p 1 n=1 a n is divergent. if l = 1, then the ratio test is. Example: determine if the series is absolute convergent, conditionally convergent, or divergent? lim ian i lim lim by the root test the series will diverge. the root test: (not covered in this course but is in the textbook) (a) if lim n i l, with 0 < l < 1 then the series an is absolutely con 00, then the series an is divergent. For series involving both powers and factorials use the ratio test (rt). example: use the root test to determine if the following series diverges or converges. Ratio test & root test let p a n be an arbitrary termed series (i.e. 1

Lecture 28 Absolute Convergence Ratio And Root Test Conditional For series involving both powers and factorials use the ratio test (rt). example: use the root test to determine if the following series diverges or converges. Ratio test & root test let p a n be an arbitrary termed series (i.e. 1
