
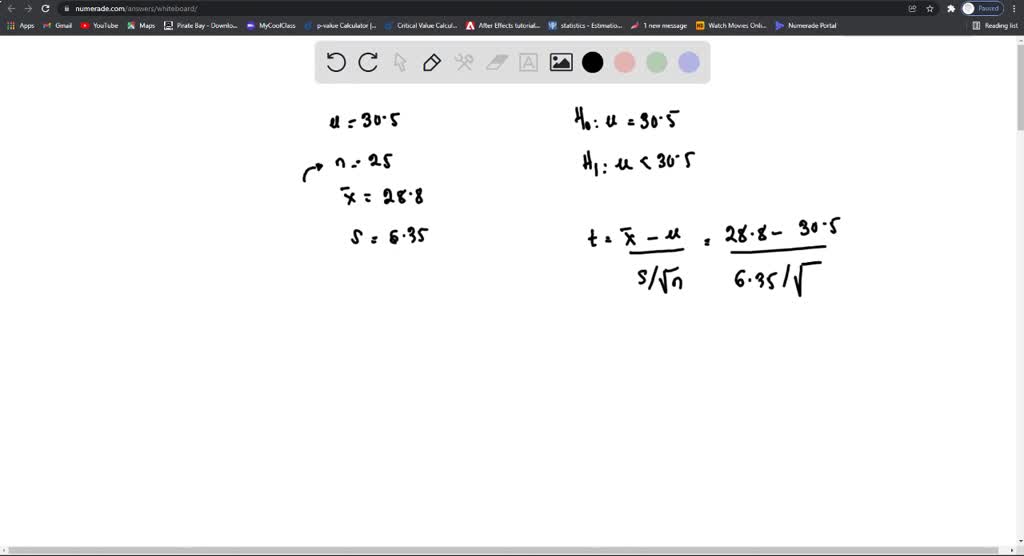
An Insurance Agent Has Claimed That The Average Age Of Policy Holders Q.11. an insurance agent has claimed that the average age of policy holders who insure through him is less than the average for all agents, which is 30.5 years. a random sample of 25 policy holders was selected with mean 28.8 years and standard deviation 6.35 years. test the agents claim at 5% level of significance. To test the insurance agent's claim, we can use a one sample t test with the null and alternative hypotheses as follows: h0: μ = 35 (the average age of policy holders who insure through the agent is equal to the average for all the agents).
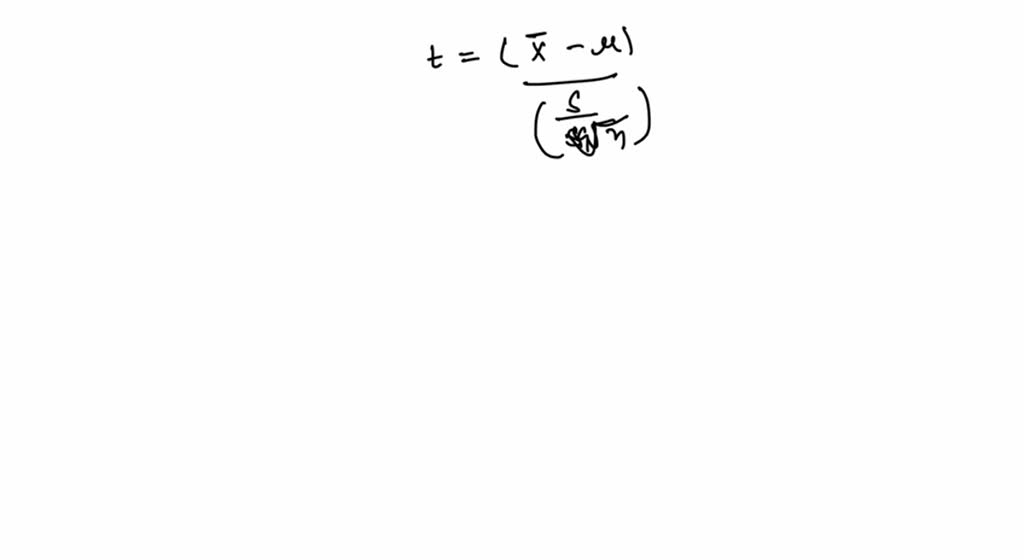
An Insurance Agent Has Claimed That The Average Age Of Policy Holders An insurance agent has claimed that the average age of policy holders who insure through him is less than the average for all agents which is 30 years. a random sample of 100 policy holders is drawn and had the average age 28 years and standard deviation 6 years. test the agent claim. q. Since calculated z ( 2.18) < critical z ( 1.645), we reject h₀. therefore, at 5% level of significance, there is sufficient evidence to support the agent's claim that the average age of his policyholders is less than the overall average of 30.5 years. 😉 want a more accurate answer?. An insurance agent has claimed that the average age of policy holders who insure through him is less than the average for all agents, which is 30 5 years. An insurance agent has claimed the average age of policyholders who insure through him is less than the average for all agents, which is 30.5 years. a random sample of 100 policyholders who had insured through him gave the following age distributions: calculate the: i.
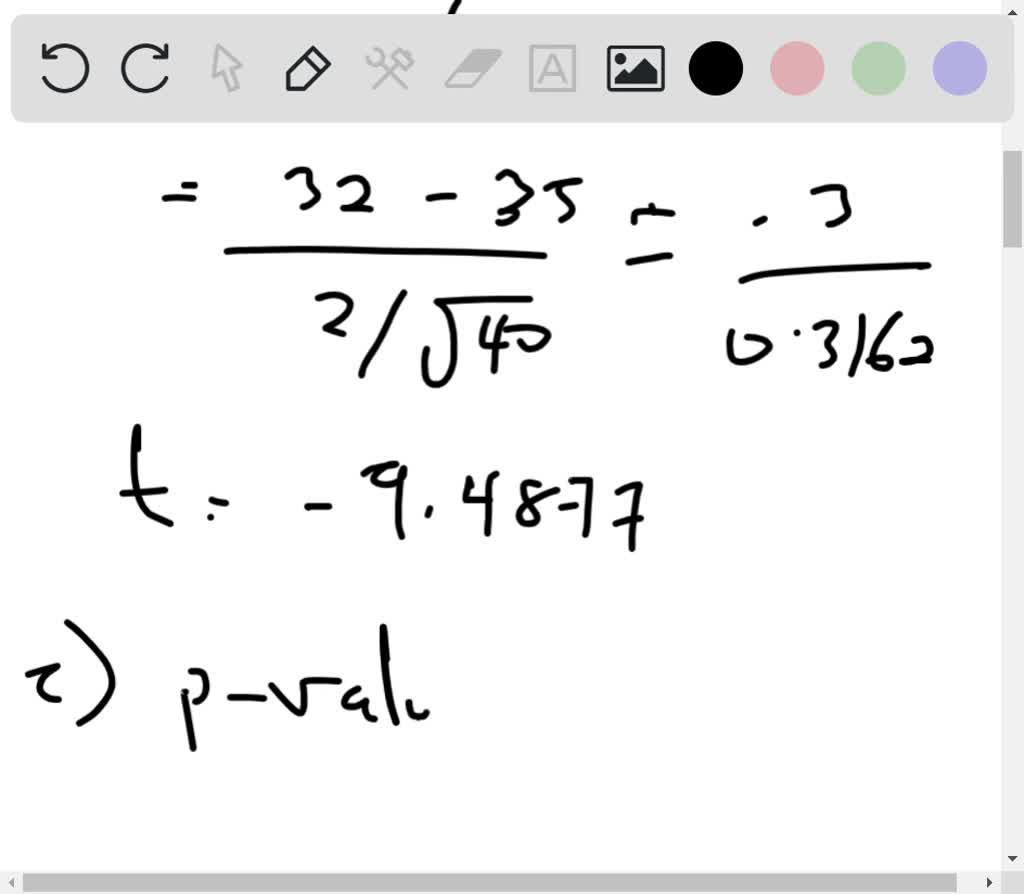
Solved An Insurance Agent Has Claimed That The Average Age Of An insurance agent has claimed that the average age of policy holders who insure through him is less than the average for all agents, which is 30 5 years. An insurance agent has claimed the average age of policyholders who insure through him is less than the average for all agents, which is 30.5 years. a random sample of 100 policyholders who had insured through him gave the following age distributions: calculate the: i. The null hypothesis (h0) is that there is no difference in the average age of policyholders between this agent and all agents, meaning the average age is 30.5 years. the alternative hypothesis (h1) is that the average age of policyholders for this agent is less show more…. Question: an insurance agent has claimed that the average age of policy holders who insure through him is less than the average for all the agents, which is 35 years. a random sample of 40 policy holders who insured through him gave an average of 32 years with the standard error of 2 years. We are testing the claim that the average age of policyholders is less than 30.5 years. z=σ nμ−μ0 where μ0=30.5, μ=28.8, σ=6.36, and n=100. z=6.36 10028.8−30.5=0.636−1.7≈−2.67. the critical z value for a 95% confidence level (one tailed test) is z=−1.645. since −2.67<−1.645, the test statistic falls in the rejection region. Null hypothesis (h0): the average age of all policy holders who insure through the agent is equal to or greater than 35 years. alternative hypothesis (h1): the average age of all policy holders who insure through the agent is less than 35 years. we will use a one sample t test to test the hypotheses.
An Insurance Agent Has Claimed That The Average Age Of Policy Holders The null hypothesis (h0) is that there is no difference in the average age of policyholders between this agent and all agents, meaning the average age is 30.5 years. the alternative hypothesis (h1) is that the average age of policyholders for this agent is less show more…. Question: an insurance agent has claimed that the average age of policy holders who insure through him is less than the average for all the agents, which is 35 years. a random sample of 40 policy holders who insured through him gave an average of 32 years with the standard error of 2 years. We are testing the claim that the average age of policyholders is less than 30.5 years. z=σ nμ−μ0 where μ0=30.5, μ=28.8, σ=6.36, and n=100. z=6.36 10028.8−30.5=0.636−1.7≈−2.67. the critical z value for a 95% confidence level (one tailed test) is z=−1.645. since −2.67<−1.645, the test statistic falls in the rejection region. Null hypothesis (h0): the average age of all policy holders who insure through the agent is equal to or greater than 35 years. alternative hypothesis (h1): the average age of all policy holders who insure through the agent is less than 35 years. we will use a one sample t test to test the hypotheses.

Solved 1 An Insurance Agent Has Claimed That The Average Chegg We are testing the claim that the average age of policyholders is less than 30.5 years. z=σ nμ−μ0 where μ0=30.5, μ=28.8, σ=6.36, and n=100. z=6.36 10028.8−30.5=0.636−1.7≈−2.67. the critical z value for a 95% confidence level (one tailed test) is z=−1.645. since −2.67<−1.645, the test statistic falls in the rejection region. Null hypothesis (h0): the average age of all policy holders who insure through the agent is equal to or greater than 35 years. alternative hypothesis (h1): the average age of all policy holders who insure through the agent is less than 35 years. we will use a one sample t test to test the hypotheses.

Solved An Medical Insurances Company Claimed That The Chegg
