An Overview Of Subset And Superset

Superset Vs Subset What S The Difference The subset relationship denotes that one set is contained within another, while the superset relationship indicates that a set includes all the elements of another set. Subset and superset are two concepts used in set theory to describe the relationship between two sets. a subset refers to a set that contains only elements that are also present in another set. in other words, all the elements of a subset are also elements of the superset.

Superset Vs Subset What S The Difference There are 2 types of subsets. supersets are those sets which satisfy the 2 condition. a ⊂ b (a subset b ) and a ≠ b (a not equal to b ). Within set theory, subsets and supersets play crucial roles in defining these relationships. in this article, we will delve into the key disparities between subsets and supersets, exploring their definitions, notations, and real world applications. A subset of a set a is any set b such that every element of b is also an element of a. a strict subset is a subset that isn't equal to the original set (i.e. b must have at least one fewer element than a). a superset of a is any set c such that a is a subset of c. It's important to note that every set is a subset of itself and a superset of itself. this is because every element in the set is contained within the set.

Sets Subset And Superset Infinity Learn By Sri Chaitanya A subset of a set a is any set b such that every element of b is also an element of a. a strict subset is a subset that isn't equal to the original set (i.e. b must have at least one fewer element than a). a superset of a is any set c such that a is a subset of c. It's important to note that every set is a subset of itself and a superset of itself. this is because every element in the set is contained within the set. A comprehensive guide on understanding the concepts of sets, subsets and supersets with examples. dive deep into the mathematical representation and application of these concepts. Definition: subset and superset let x be a set. a set a is called a subset of x and denoted by a ⊆ x, if each element of a is also an element of x. equivalently, x is a superset of a, denoted as x ⊇ a. The relationship between sets, a subset, a superset, and an element plays a crucial role in understanding set theory. a subset, denoted as a ⊆ b, represents a set whose elements are also elements of another set, b. If a is a subset of b and b is a subset of c, then a is also a subset of c. any set a is a superset of the empty set, and any other set is a superset of that set.

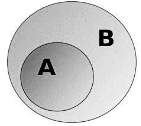
An Overview Of Subset And Superset A comprehensive guide on understanding the concepts of sets, subsets and supersets with examples. dive deep into the mathematical representation and application of these concepts. Definition: subset and superset let x be a set. a set a is called a subset of x and denoted by a ⊆ x, if each element of a is also an element of x. equivalently, x is a superset of a, denoted as x ⊇ a. The relationship between sets, a subset, a superset, and an element plays a crucial role in understanding set theory. a subset, denoted as a ⊆ b, represents a set whose elements are also elements of another set, b. If a is a subset of b and b is a subset of c, then a is also a subset of c. any set a is a superset of the empty set, and any other set is a superset of that set.

Superset Png Images Pngegg The relationship between sets, a subset, a superset, and an element plays a crucial role in understanding set theory. a subset, denoted as a ⊆ b, represents a set whose elements are also elements of another set, b. If a is a subset of b and b is a subset of c, then a is also a subset of c. any set a is a superset of the empty set, and any other set is a superset of that set.