
Solved 1 Find F 1 F 2 F 3 F 4 And F 5 If F Is Chegg There are 2 steps to solve this one. here, reference the values that can be present in the graph and use the given graph to estimate the value of each derivative. (i) (a) f ′(−3) (b) f ′(−2) (c) f ′(−1) (d) f ′(0) (e) f ′(1) (f) f ′(2) (9) f ′(3) sketch the graph of f ′. use the given graph to estimate the value of each derivative. Subscribe to verify your answer subscribe save to notebook! sign in to save notes sign in verify. save. show steps . hide steps . number line. related. functions examples. y=\frac{x^2 x 1}{x} f(x)=x^3 ; f(x)=\ln (x 5) f(x)=\frac{1}{x^2} y=\frac{x}{x^2 6x 8} f(x)=\sqrt{x 3}.
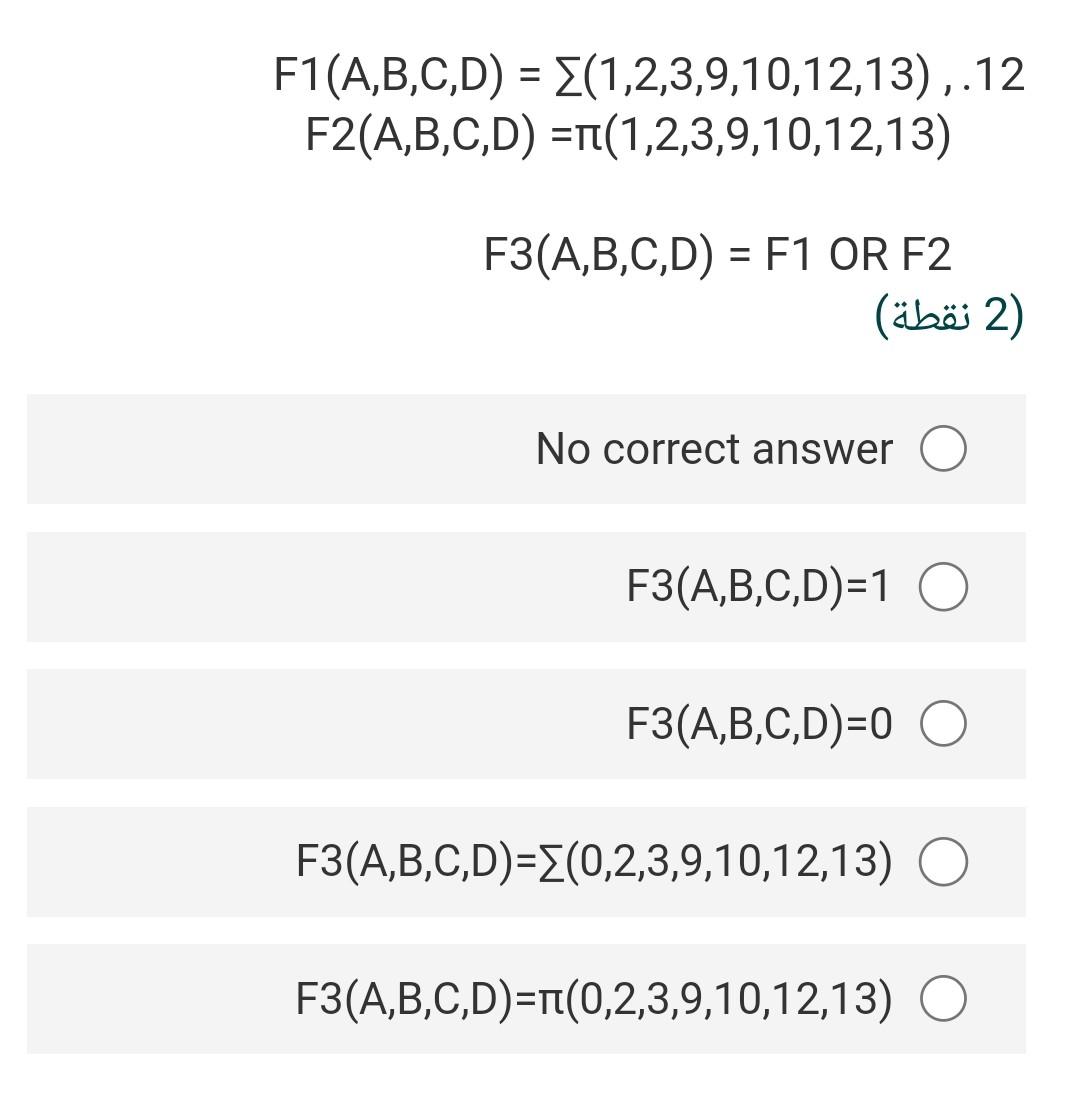
Solved F1 A B C D 1 2 3 9 10 12 13 12 F2 A B C D Chegg Free math problem solver answers your algebra homework questions with step by step explanations. From the graph shown, find: a. f ( 1) b. f (0) c. 3f (2) d. the value of x that corresponds to f (x)=0. given a function f, an interval [a,b] and a value v. find a value c in the interval so that f (c)=v. apply the intermediate value theorem. (a)f (x)=x2f (x)=x2 on [0,3], v = 2 (b)f (x)=sinx on [0,π2],v=12f (x)=sinx on [0,π2],v=12. Suppose that f is an even function whose domain is the set of all real numbers. then which of the following can we claim to be true? a. the function has an inverse f^ 1 that is odd. c. we can't tell whether or not f has an inverse. d. the function f has an inverse f^ 1, but we can't tell whether it's even or odd. e. Quickly check that $$ f(x y) = a(x y) b = ax b y = f(x) y \neq f(x) f(y), $$ so the constant $b$ stops $f$ from being linear. this means that all you're left with is $f(x) = ax$, so only option $(b)$ satisfies this.
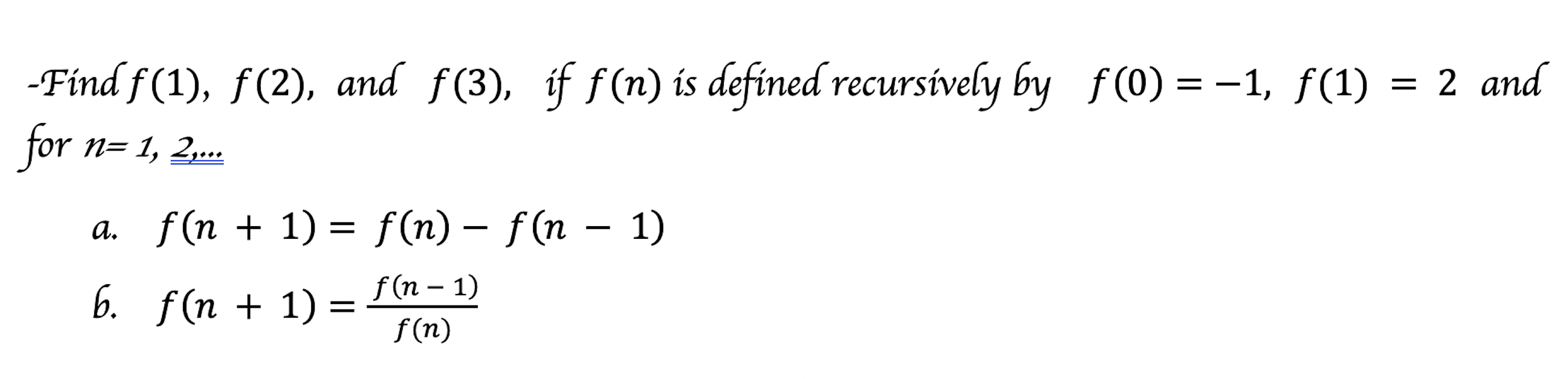
Solved Find F 1 F 2 And F 3 If F N Is Defined Chegg Suppose that f is an even function whose domain is the set of all real numbers. then which of the following can we claim to be true? a. the function has an inverse f^ 1 that is odd. c. we can't tell whether or not f has an inverse. d. the function f has an inverse f^ 1, but we can't tell whether it's even or odd. e. Quickly check that $$ f(x y) = a(x y) b = ax b y = f(x) y \neq f(x) f(y), $$ so the constant $b$ stops $f$ from being linear. this means that all you're left with is $f(x) = ax$, so only option $(b)$ satisfies this. There are 2 steps to solve this one. the graph of the function f (x) is given. not the question you’re looking for? post any question and get expert help quickly. Let f be a function from a to b, whose graph is gf = f(0;0);(1;2);(2;4);(3;6);(4;8)g (a) give the range of f. f0;2;4;6;8g (b) if the inverse, f 1, exists, give it as a set of ordered pairs. if it does not exist, say why not. the inverse does not exist because the function f is not onto. (c) let g(x) = jx 2 k be a function from b to a i. give. Answer to (a) f'( 3)(b) f'( 2)(c) f'( 1)(d) f'(0)(e) f'(1)(f) f. Interval [0,1] and f(x) > 0 for every 0 ≤ x ≤ 1. prove that the reciprocal function 1 f: [0,1] → r is bounded on [0,1]. (b) does this result remain true if: (i) f: [0,1] → r is not continuous on [0,1]; (ii) f: (0,1) → r is continuous on the open interval (0,1)? solution. • (a) let m = inf x∈[0;1] f(x). since f > 0 on [0,1], we.
