
16 Identify Complementary Supplementary Vertical Adjacent And Congruent When sum of two adjacent angles is 180°, they are called linear pair of angles. or, we can say when supplementary angles formed on a straight line, those angles are called a linear pair of angles. in the above diagram, ∠abo ∠cbo = 180°, therefore, they form a linear pair of angles. 1) find the value of x. 2) find the ∠por. A step by step guide to finding complementary, supplementary, vertical, adjacent, and congruent angles. when two angles are paired, then there exist different angles such as: 1. complementary angles. if the sum of the two angles reaches \(90\) degrees, they are called complementary angles.

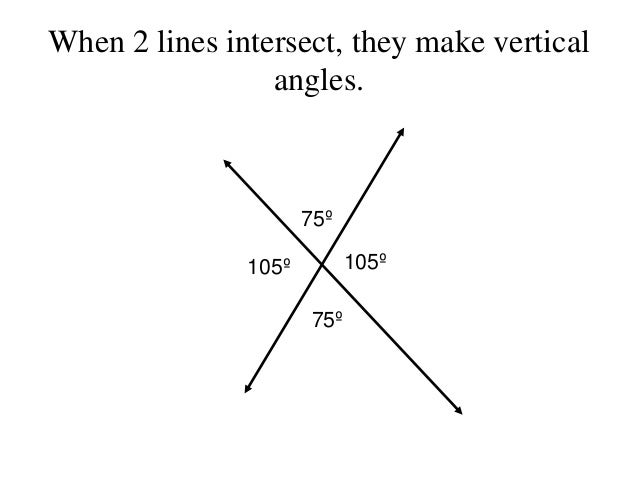
Answered Adjacent Angles Vertical Angles Linear Pairs Complementary Vertical angles are opposite angles; they share only their vertex point. two intersecting lines create two pairs of vertical angles. see if you can spot them in our drawing. did you find ∠jyo and ∠kyc made a pair? they touch only at point y. did you find ∠kyj and ∠oyc made the other pair? they also touch only at point y. Use supplementary, complementary, vertical, and adjacent angles to find unknown angles (7.g.5) adjacent angles: angles that share a common side and have the same vertex. vertical angles: opposite angles formed by the intersection of 2 lines. they are congruent angles. congruent angles; angles that have the same measure. Complementary angles are two positive angles whose sum is 90 degrees. for example, complementary angles can be adjacent, as seen in with ∠abd and ∠cbd in the image below. or they can be two acute angles, like ∠mnp and ∠efg, whose sum is equal to 90 degrees. both of these graphics represent pairs of complementary angles. 2. supplementary angles. Two or more angles can be related, if certain conditions are met. here, we will learn different types of angle relationships. (i) congruent angles (ii) vertical angles (iii) complementary angles (iv) supplementary angles (v) adjacent angles (vi) adjacent angles in parallelogram (vii) linear pair (viii) corresponding angles.
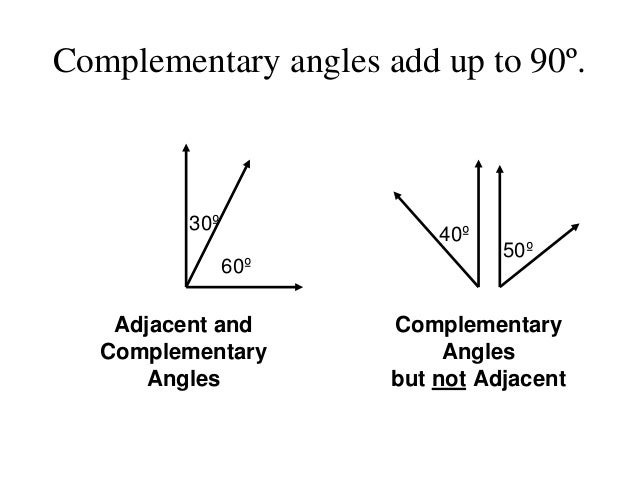
Angle Pairs Complementary Supplementary Adjacent Vertical Linear Complementary angles are two positive angles whose sum is 90 degrees. for example, complementary angles can be adjacent, as seen in with ∠abd and ∠cbd in the image below. or they can be two acute angles, like ∠mnp and ∠efg, whose sum is equal to 90 degrees. both of these graphics represent pairs of complementary angles. 2. supplementary angles. Two or more angles can be related, if certain conditions are met. here, we will learn different types of angle relationships. (i) congruent angles (ii) vertical angles (iii) complementary angles (iv) supplementary angles (v) adjacent angles (vi) adjacent angles in parallelogram (vii) linear pair (viii) corresponding angles. Angle pairs are essential in geometry for measuring and classifying angles. they comprise four primary entities: complementary angles, supplementary angles, vertical angles, and adjacent angles. complementary angles are two angles that add up to 90 degrees, while supplementary angles add up to 180 degrees. Some examples are complementary angles, supplementary angles, vertical angles, alternate interior angles, alternate exterior angles, corresponding angles and adjacent angles. pairs of angles are formed when two lines intersect or when a transversal line crosses two or more other lines. understanding these pairs is crucial in geometry. Identify complementary, supplementary angles, vertical angles, and adjacent angles; apply angle relationships to solve for unknown angles in a diagram; write equations to solve for unknown angles using angle pair relationships; explain real life applications of angle relationships. Adjacent angles are two angles that share a common vertex and side, but have no common interior points. ∠5 and ∠6 are adjacent angles. ∠7 and ∠8 are nonadjacent angles. complementary angles are two positive angles whose measures have a sum of 90°. each angle is the complement of the other.
Angle Pairs Complementary Supplementary Adjacent Vertical Linear Angle pairs are essential in geometry for measuring and classifying angles. they comprise four primary entities: complementary angles, supplementary angles, vertical angles, and adjacent angles. complementary angles are two angles that add up to 90 degrees, while supplementary angles add up to 180 degrees. Some examples are complementary angles, supplementary angles, vertical angles, alternate interior angles, alternate exterior angles, corresponding angles and adjacent angles. pairs of angles are formed when two lines intersect or when a transversal line crosses two or more other lines. understanding these pairs is crucial in geometry. Identify complementary, supplementary angles, vertical angles, and adjacent angles; apply angle relationships to solve for unknown angles in a diagram; write equations to solve for unknown angles using angle pair relationships; explain real life applications of angle relationships. Adjacent angles are two angles that share a common vertex and side, but have no common interior points. ∠5 and ∠6 are adjacent angles. ∠7 and ∠8 are nonadjacent angles. complementary angles are two positive angles whose measures have a sum of 90°. each angle is the complement of the other.
