Answered Consider The Following Three Systems Of Bartleby Consider the following system of linear equations. (a) use elementary row operations to determine the augmented matrix in reduced row echelon form. (b) how many solutions are there to this system?. When a general system of linear equations has exactly one solution, it is called consistent and independent. in this case, each line in the system intersects at exactly one point; thus, the system is also linearly independent. finally, when a system of linear equations has infinitely many solutions, it is called consistent and dependent.
Answered Consider The Following Three Systems Of Bartleby Dear @jeff, also add a ≠ −1 a ≠ − 1 for (i). no, actual there are only 3 variables. a is a parameter. you shall solve this system dependent on a, that means your solution will depend on the parameter a. after that, you should say, which values of a are suitable for the three possibilities (i), (ii), (iii). hint:. For the system of linear equations: x − 2y = 1, x − y kz = −2, ky 4z = 6,k ∈ r consider the following statements: (a) the system has unique solution if k ≠ 2,k ≠ −2 (b) the system has unique solution if k = 2. (c) the system has unique solution if k = 2. (d) the system has no solution if k = 2. Consider the following system of linear equations (2 1 − 4 4 3 − 12 1 2 − 8) (x y z) = (α 5 7) notice that the second and the third columns of the coefficient matrix are linearly dependent. for how many values of α, does this system of equations have infinitely many solutions?. There will be unique solution. answer is 1. consider the following system of equations: $3x 2y = 1 $ $4x 7z = 1 $ the number of solutions for this system is.

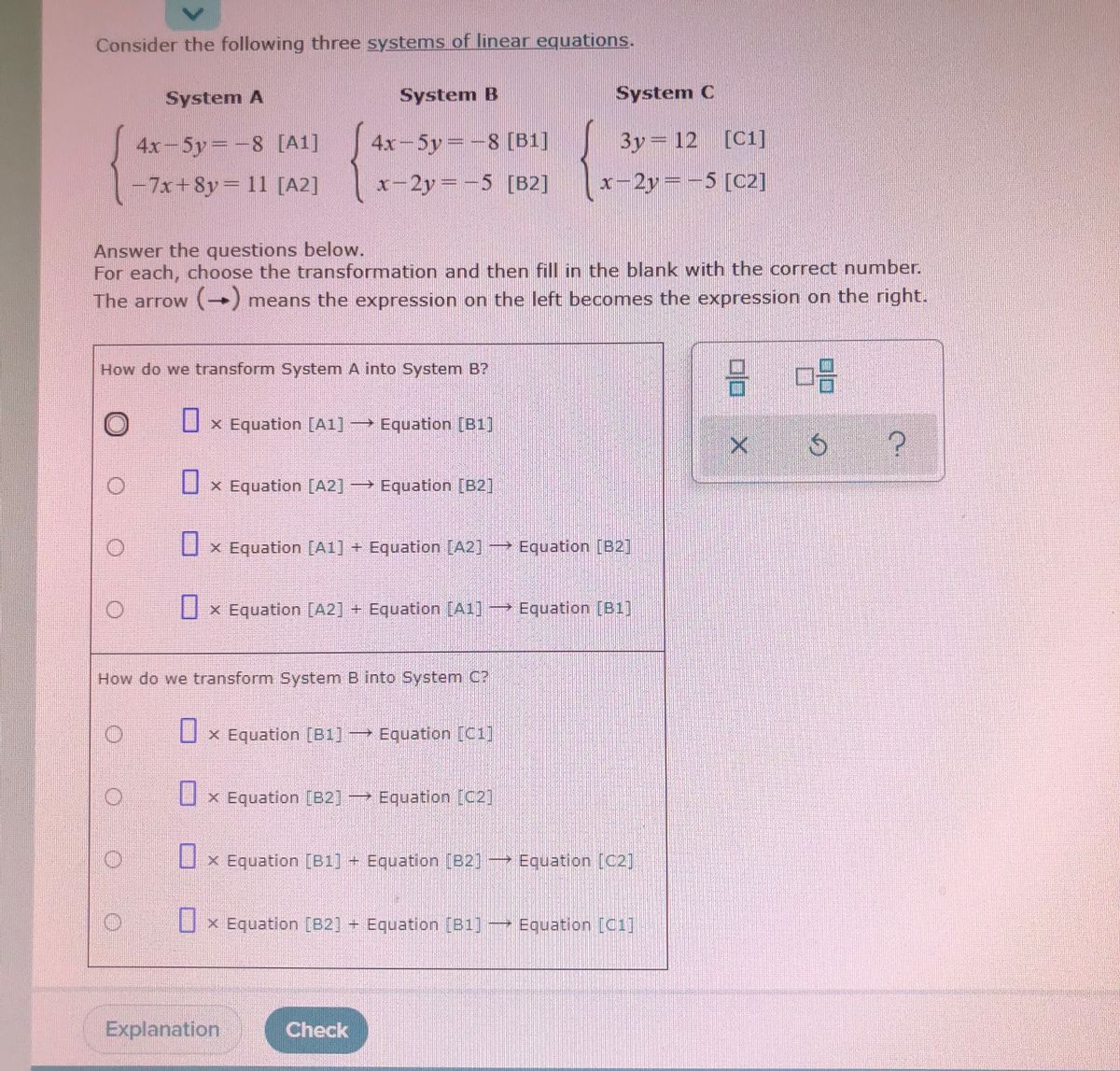
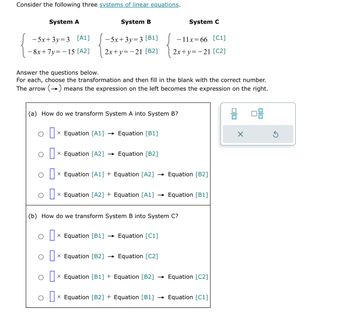
Answered 1 Consider The Following System Of Bartleby Consider the following system of linear equations (2 1 − 4 4 3 − 12 1 2 − 8) (x y z) = (α 5 7) notice that the second and the third columns of the coefficient matrix are linearly dependent. for how many values of α, does this system of equations have infinitely many solutions?. There will be unique solution. answer is 1. consider the following system of equations: $3x 2y = 1 $ $4x 7z = 1 $ the number of solutions for this system is. Q: solve the system of linear equations in terms of a, where a = y. 2x 2y z=1 2x 2y z=1 a: we are given system of equations as q: determine whether a system of two linear equations with (0,0) and (2,2) as solutions. Consider the following system of equations. since the two lines are in a system we deal with them together by graphing them on the same coordinate axes. the lines can be graphed using your favorite method. lets graph by making a table of values for each line. a solution for a single equation is any point that lies on the line for that equation. Consider the following system of linear algebraic equations. elimination systematically eliminates variables from a subset of equations to identify a subproblem of lower dimension. back substitution systematically uses any solution for the lower dimensional subproblem to find a solution for the eliminated variables in the higher order problem. Answer the questions below. for each, choose the transformation and then fill in the blank with the correct number. the arrow (→) means the expression on the left becomes the expression on the right. (a) how do we transform system a into system b?.
