Answered U 3 5 And V 2 1 Determine Whether U And V Are Parallel Kunduz

Answered U 3 5 And V 2 1 Determine Whether U And V Are Parallel Kunduz U 3 5 and v 2 1 determine whether u and v are parallel orthogonal or neither hect one da orthogonal o b parall > receive answers to your questions. To determine whether the vectors u and v are orthogonal, parallel, or neither, we need to perform two tests: dot product test (orthogonality test): if the dot product of two vectors is zero, then the vectors are orthogonal (perpendicular to each other).

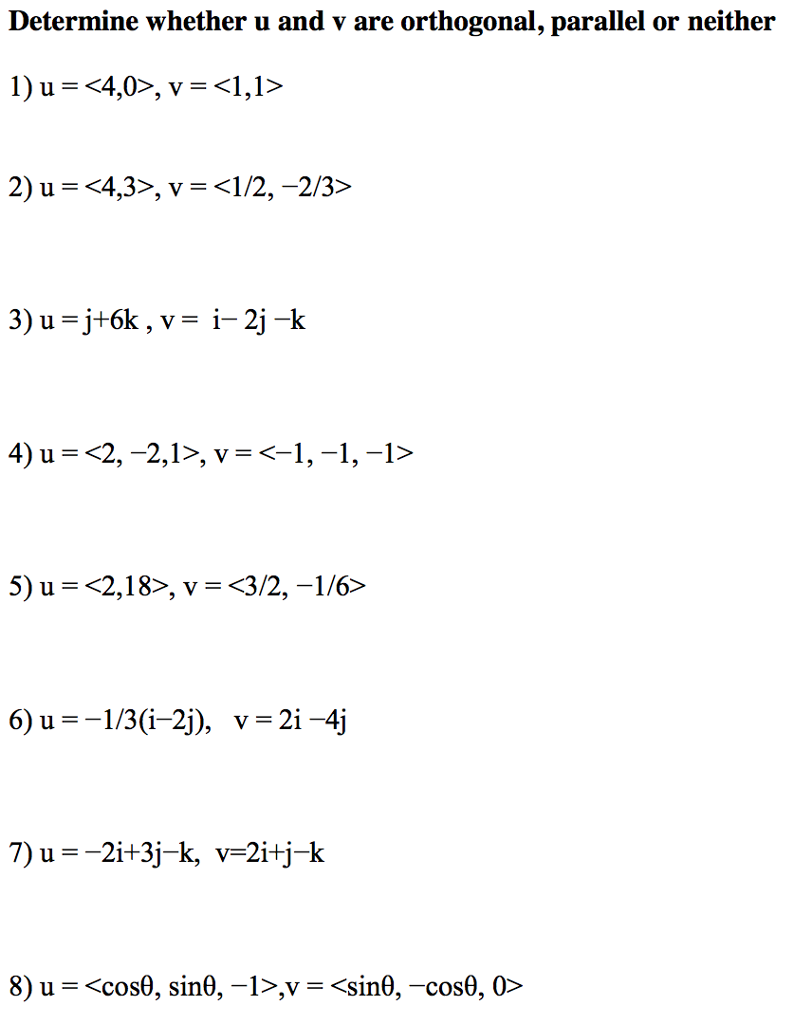
Solved Determine Whether U And V Are Orthogonal Parallel Or Chegg Scalar multiples are fundamental when discussing vector parallelism. two vectors are parallel if one is a scalar multiple of the other. this means that one vector can be obtained by scaling another vector by some real number. The definitions of orthogonal and parallel vectors are based on their dot product and scalar multiples. a dot product of zero indicates orthogonality, while being scalar multiples confirms parallelism. Exercise 4.1.7 determine whether u and v are parallel in each of the following cases. a. u= 3 6 3. v= 5 10 5 3 1 2 b. u= v = 6 3 2 1 1 g c. u= 3 0 1 1 d. u= 2 0 1 v= 8 0 4. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. In fact, a vector is parallel to $u$ if and only if it has this property. equivalently, the vectors that are parallel to $u$ are precisely those vectors along the green line, that is, whose coordinates satisfy the equation $2y = x$.

Solved Let U 5 2 1 V 4 3 0 W 22 5 S 1 Determine The Chegg Exercise 4.1.7 determine whether u and v are parallel in each of the following cases. a. u= 3 6 3. v= 5 10 5 3 1 2 b. u= v = 6 3 2 1 1 g c. u= 3 0 1 1 d. u= 2 0 1 v= 8 0 4. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. In fact, a vector is parallel to $u$ if and only if it has this property. equivalently, the vectors that are parallel to $u$ are precisely those vectors along the green line, that is, whose coordinates satisfy the equation $2y = x$. ### summary: to determine if two vectors are parallel, calculate their scalar product. if the scalar product is zero, the vectors are parallel. if the scalar product is not zero, the vectors are not parallel. Since the dot product is 0, the two vectors are orthogonal. they are not parallel, since they are not linear multiples of one another. still looking for help? get the right answer, fast. get a free answer to a quick problem. most questions answered within 4 hours. choose an expert and meet online. Find step by step calculus solutions and the answer to the textbook question determine whether u and v are orthogonal, parallel, or neither. u = 1 3 (i 2j), v = 2i 4j. In our exercise, we tried to find a scalar that can transform u into v but couldn't, hence concluding that the vectors are not parallel. this process emphasizes the concept that parallel vectors must be scalable versions of each other, keeping the vector direction intact while varying the magnitude.

Answered Determine Whether The Vectors U And V Are Parallel Kunduz ### summary: to determine if two vectors are parallel, calculate their scalar product. if the scalar product is zero, the vectors are parallel. if the scalar product is not zero, the vectors are not parallel. Since the dot product is 0, the two vectors are orthogonal. they are not parallel, since they are not linear multiples of one another. still looking for help? get the right answer, fast. get a free answer to a quick problem. most questions answered within 4 hours. choose an expert and meet online. Find step by step calculus solutions and the answer to the textbook question determine whether u and v are orthogonal, parallel, or neither. u = 1 3 (i 2j), v = 2i 4j. In our exercise, we tried to find a scalar that can transform u into v but couldn't, hence concluding that the vectors are not parallel. this process emphasizes the concept that parallel vectors must be scalable versions of each other, keeping the vector direction intact while varying the magnitude.