
Solution Angle Au Centre Et Angle Inscrit Fiches Pedagogiques Maths 1 Etapes de la construction d'un arc capable, arc capable, angle orienté, angle inscrit, angle au centre, construction d'un arc capable, maths,. Construction d'un arc capable : on trace la médiatrice de [bc]; soit ^bct de mesure α; on trace la perpendiculaire à (ct) passant par c. elle coupe la médiatrice de [bc] en o; on trace le cercle de centre o passant par a; l'arc capable de l'angle α est l'arc interceptant [bc] non contenu dans ^bct.
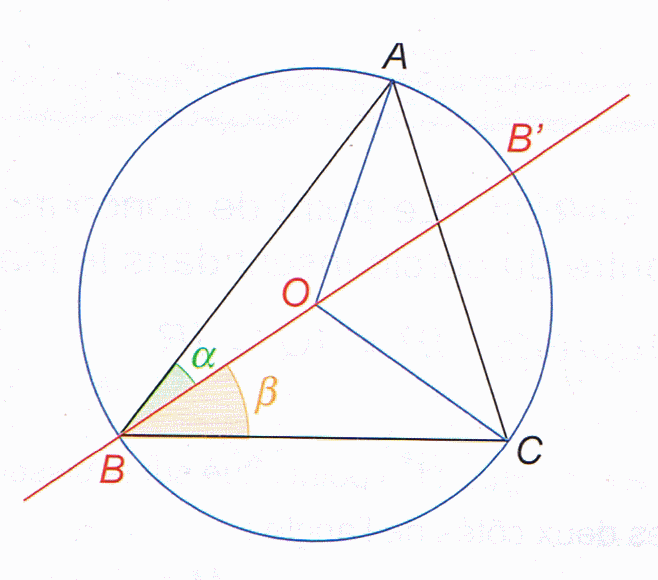
Angle Inscrit Angle Au Centre Forum De Maths 242331 L’arc capable (en réalité le double arc capable) relatif à un segment ab et à un angle est le lieu géométrique des points d’où l’on “voit” le segment ab sous l’angle : § 2. On dit que le segment [ab] est vu depuis l'arc sous l'angle α ou encore que l'arc ⌢ est capable d'inscrire un angle de la mesure α. le théorème de l'arc capable est très lié au théorème de l'angle inscrit dont on peut considérer qu'il est la réciproque. 5. le théorème de l'arc capable. soit un angle ∈ ]0; [ et deux points a et b donnés. le lieu l des points m du plan tels que amb= , s'appelle arc capable, c'est l'ensemble des points d'où l'on voit le segment [ab] selon un angle . remarquons que l par rapport à (ab). a) l n'est pas vide. La vidéo présente le concept d'arc capable et explique comment on peut construire facilement un arc capable.
Problème Angle Inscrit Angle Au Centre Forum Mathématiques 5. le théorème de l'arc capable. soit un angle ∈ ]0; [ et deux points a et b donnés. le lieu l des points m du plan tels que amb= , s'appelle arc capable, c'est l'ensemble des points d'où l'on voit le segment [ab] selon un angle . remarquons que l par rapport à (ab). a) l n'est pas vide. La vidéo présente le concept d'arc capable et explique comment on peut construire facilement un arc capable. Inscrit l’angle. on peut en déduire qu’il vaut 90° car, par définition du théorème, il vaut la moitié de l’angle au centre qui intercepte le même arc, donc 180 2=90°. On peut justifier ce théorème à l'aide du théorème de l'angle inscrit. la construction à la règle, au compas et au rapporteur ( ou bien avec geogebra ) de ces arcs de cercle demande une petite réflexion . On appelle angle inscrit l’angle de sommet un point du cercle, et dont les côtés passent par deux points du cercle on dit que deux angles interceptent le même arc l’intersection demi–droite : [ax) segment de droite [ab]. Dans un cercle, si un angle au centre et un angle inscrit interceptent le même arc, alors la mesure de l’angle au centre est le double de celle de l'angle inscrit. démonstration : fait en activité.
