
Mths221 Note 18 The Ratio Test Root Test And Absolute And Definition: a series an is divergent and the series theorem: if a series an is called absolutely convergent if the series a is is called conditionally convergent if the series an is convergent. is absolutely convergent, then it is convergent. example: determine if the series is absolutely convergent, conditionally convergent, or divergent?. Definition of absolute and condition convergence; examples of testing series for absolute convergence, conditional converge, or divergence. statement and var.

Root And Ratio Test Absolute Convergence Lecture Notes Math 231 Example 11.7.2. the ratio test is particularly useful for series involving the factorial function. consider \(\sum {n=0}^\infty 5^n n!\). \[ \lim {n\to\infty} {5^{n 1}\over (n 1)!}{n!\over 5^n}= \lim {n\to\infty} {5^{n 1}\over 5^n}{n!\over (n 1)!}= \lim {n\to\infty} {5}{1\over (n 1)}=0. \nonumber \] since \(0 < 1\), the series converges. Theorem (root test). let l = lim n!¥ n p janj= janj 1 n, if it exists. there are three possibilities, with the same conclusions as the ratio test: •if l < 1 then åan is absolutely convergent •if l > 1 then åan is divergent •if l = 1 then the root test is inconclusive sketch proof. if l < 1 then janjˇln for sufficiently large n. we. Example 2 ratio test let p 1 n=1 a n be a series (the terms may be positive or negative). let l = lim n!1 an 1 an . if l < 1, then the series p 1 n=1 a n converges absolutely. if l > 1 or 1, then the series p 1 n=1 a n is divergent. if l = 1, then the ratio test is inconclusive. example 2 test the following series for convergence x1 n=1 ( 1)n n. The root test (rot): let ∑ be a series of nonzero terms and suppose lim | | . (i) if 1, the series converges absolutely. (ii) if 1, the series diverges. (iii) if 1, the test is inconclusive. 1. for any type of series: positive, alternating, or other. 2. if 1, the test fails. you must use a different test. 3.

Ap Calculus Bc 10 06 Ratio And Root Test For Convergence Of Series Example 2 ratio test let p 1 n=1 a n be a series (the terms may be positive or negative). let l = lim n!1 an 1 an . if l < 1, then the series p 1 n=1 a n converges absolutely. if l > 1 or 1, then the series p 1 n=1 a n is divergent. if l = 1, then the ratio test is inconclusive. example 2 test the following series for convergence x1 n=1 ( 1)n n. The root test (rot): let ∑ be a series of nonzero terms and suppose lim | | . (i) if 1, the series converges absolutely. (ii) if 1, the series diverges. (iii) if 1, the test is inconclusive. 1. for any type of series: positive, alternating, or other. 2. if 1, the test fails. you must use a different test. 3. Ratio test suppose p a n is a series for which the limit l= lim n!1 a n 1 a n exists (possibly l= 1). then if l<1 then the series p a n is absolutely convergent. if l>1 then the series p a n is divergent. if l= 1 then the ratio test is inconclusive. Ratio test theorem (ratio test) given x∞ k=1 ak, with ak ̸= 0 for all k, suppose that lim k→∞ ak 1 ak = l. then 1. if l <1, the series converges absolutely, 2. if l >1, the series diverges, 3. if l = 1, there is no conclusion. [#6 p.719] ratio test: 1. if lim n!1 an 1 an = l < 1, then the series ∑1 n=1 an is absolutely convergent. 2. if lim n!1 an 1 an = l > 1 or lim n!1 an 1 an = 1, then the series ∑1 n=1 an is divergent. 3. if lim n!1 an 1 an = 1, the ratio test is inconclusive; that is, no conclusion can be drawn about the convergence or divergence of ∑1 n=1. Absolute convergence, ratio and root test. (section 11.6 in stewart) in this lecture we will develop the tools necessary to tackle the problem of nding the radius of con vergence of a power series. in particular, we will develop two further tests for convergence, namely the ratio test and the root test.

5 6 2 Convergence Tests The Root Test Guide Pdf Mth 201 Chapter 5 Ratio test suppose p a n is a series for which the limit l= lim n!1 a n 1 a n exists (possibly l= 1). then if l<1 then the series p a n is absolutely convergent. if l>1 then the series p a n is divergent. if l= 1 then the ratio test is inconclusive. Ratio test theorem (ratio test) given x∞ k=1 ak, with ak ̸= 0 for all k, suppose that lim k→∞ ak 1 ak = l. then 1. if l <1, the series converges absolutely, 2. if l >1, the series diverges, 3. if l = 1, there is no conclusion. [#6 p.719] ratio test: 1. if lim n!1 an 1 an = l < 1, then the series ∑1 n=1 an is absolutely convergent. 2. if lim n!1 an 1 an = l > 1 or lim n!1 an 1 an = 1, then the series ∑1 n=1 an is divergent. 3. if lim n!1 an 1 an = 1, the ratio test is inconclusive; that is, no conclusion can be drawn about the convergence or divergence of ∑1 n=1. Absolute convergence, ratio and root test. (section 11.6 in stewart) in this lecture we will develop the tools necessary to tackle the problem of nding the radius of con vergence of a power series. in particular, we will develop two further tests for convergence, namely the ratio test and the root test.
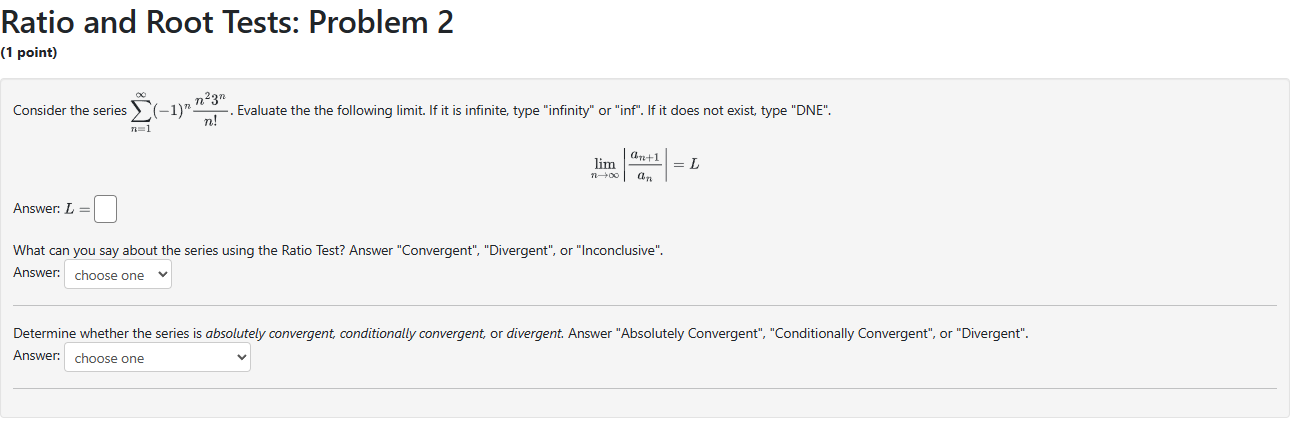
Solved Ratio And Root Tests Problem 2 1 Point Consider Chegg [#6 p.719] ratio test: 1. if lim n!1 an 1 an = l < 1, then the series ∑1 n=1 an is absolutely convergent. 2. if lim n!1 an 1 an = l > 1 or lim n!1 an 1 an = 1, then the series ∑1 n=1 an is divergent. 3. if lim n!1 an 1 an = 1, the ratio test is inconclusive; that is, no conclusion can be drawn about the convergence or divergence of ∑1 n=1. Absolute convergence, ratio and root test. (section 11.6 in stewart) in this lecture we will develop the tools necessary to tackle the problem of nding the radius of con vergence of a power series. in particular, we will develop two further tests for convergence, namely the ratio test and the root test.
