
Solved Determine Whether The Series Is Absolutely Convergent There are times when we can (i.e. the series is absolutely convergent) and there are times when we can’t (i.e. the series is conditionally convergent). as a final note, the fact above tells us that the series,. Determine whether the series \(\displaystyle\sum {n=1}^{\infty}\displaystyle\frac{( 1)^n}{9n 5}\) is absolutely convergent, conditionally convergent, or divergent; justify your answer.

Solved 4 Are The Following Series Absolutely Convergent Chegg Series that are absolutely convergent are guaranteed to be convergent. however, series that are convergent may or may not be absolutely convergent. let’s take a quick look at a couple of examples of absolute convergence. example 1 determine if each of the following series are absolute convergent, conditionally convergent or divergent. For each of the following series determine if they are absolutely convergent, conditionally convergent or divergent. here is a set of practice problems to accompany the absolute convergence section of the series & sequences chapter of the notes for paul dawkins calculus ii course at lamar university. Determine whether the given series is absolutely convergent, conditionally convergent, or diverges. name any convergence test(s) that you use, and justify all of your work. 2. x∞ n=1 (−1)n 5n 3 1st x∞ n=1 (−1)n 5n 3,−→ x∞ n=1 1 5n 3 ≈ x∞ n=1 1 n a.s. ↙2nd diverges. p series harmonic p = 1 1. b n = 1 5n 3 > 0 2. lim n→. Conditional convergence definition an infinite series x∞ k=1 ak is conditionally convergent if the series converges but the series x∞ k=1 |ak|diverges. for an arbitrary series x∞ k=1 ak, the series may be classified in only one of the following ways: absolutely convergent conditionally convergent divergent.
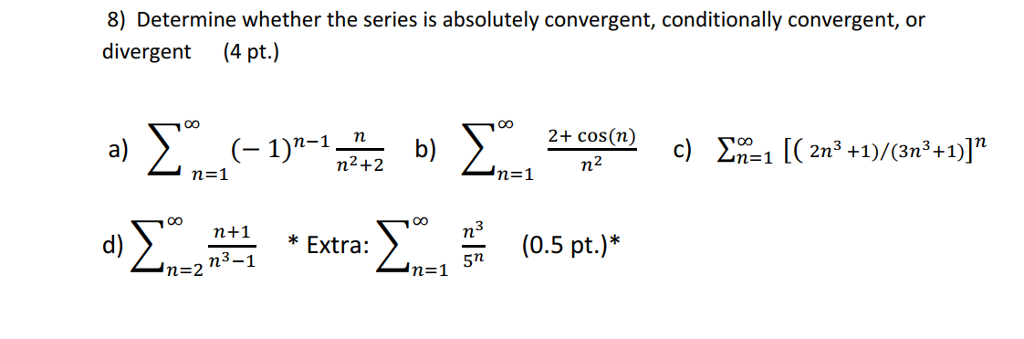
Solved 8 Determine Whether The Series Is Absolutely Chegg Determine whether the given series is absolutely convergent, conditionally convergent, or diverges. name any convergence test(s) that you use, and justify all of your work. 2. x∞ n=1 (−1)n 5n 3 1st x∞ n=1 (−1)n 5n 3,−→ x∞ n=1 1 5n 3 ≈ x∞ n=1 1 n a.s. ↙2nd diverges. p series harmonic p = 1 1. b n = 1 5n 3 > 0 2. lim n→. Conditional convergence definition an infinite series x∞ k=1 ak is conditionally convergent if the series converges but the series x∞ k=1 |ak|diverges. for an arbitrary series x∞ k=1 ak, the series may be classified in only one of the following ways: absolutely convergent conditionally convergent divergent. The following test is useful for determining whether a given series is absolutely convergent, and it will be used often in section 10.8 when we want to determine where a power series converges. it says that we can be certain that a given series is absolutely convergent, if the limit of the ratios of successive terms has a value less than 1. If c < 1, the series p a n is absolutely convergent (and hence convergent); if c > 1, the series p a n is divergent; if c = 1, the series p a n may be divergent, conditionally convergent, or absolutely convergent. proof. first note that we can assume without loss of generality that the series will start at n = 1. if c < 1, there is a number r. The series $\sum a n$ is: absolutely convergent if $\sum |a n|$ converges. conditionally convergent if $\sum |a n|$ diverges but $\sum a n$ converges. divergent if $\sum |a n|$ diverges but $\sum a n$ also diverges. let me know if the resume of these rules is ok. following these rules then:. Answer: convergent. 18. determine whether the series is absolutely convergent, conditionally convergent, or divergent. 3.

Solved For 1 And 2 Determine Whether The Series Is Chegg The following test is useful for determining whether a given series is absolutely convergent, and it will be used often in section 10.8 when we want to determine where a power series converges. it says that we can be certain that a given series is absolutely convergent, if the limit of the ratios of successive terms has a value less than 1. If c < 1, the series p a n is absolutely convergent (and hence convergent); if c > 1, the series p a n is divergent; if c = 1, the series p a n may be divergent, conditionally convergent, or absolutely convergent. proof. first note that we can assume without loss of generality that the series will start at n = 1. if c < 1, there is a number r. The series $\sum a n$ is: absolutely convergent if $\sum |a n|$ converges. conditionally convergent if $\sum |a n|$ diverges but $\sum a n$ converges. divergent if $\sum |a n|$ diverges but $\sum a n$ also diverges. let me know if the resume of these rules is ok. following these rules then:. Answer: convergent. 18. determine whether the series is absolutely convergent, conditionally convergent, or divergent. 3.
