Change Of Basis Matrix Pdf Learn how to convert vectors from one basis to another using a change of basis formula and a change of basis matrix. see examples of change of basis in finite dimensional vector spaces and applications in physics. Learn how to switch from one basis to another in a vector space and how it affects coordinate vectors and linear operators. find formulas, proofs and examples with solutions.
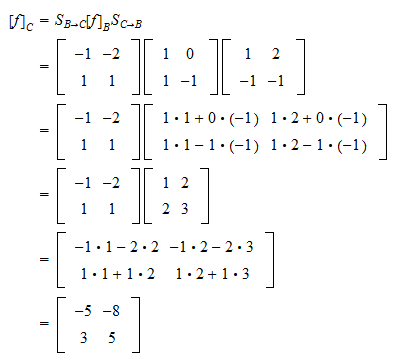
Change Of Basis Formula Examples Proofs Learn how to express a vector in a vector space as a linear combination of a basis and how to change the basis. see definitions, theorems, examples, and exercises on change of basis. The matrix \(p\) is called a \(\textit{change of basis}\) matrix. there is a quick and dirty trick to obtain it: look at the formula above relating the new basis vectors \(v' {1},v' {2},\ldots v' {n}\) to the old ones \(v {1},v {2},\ldots,v {n}\). in particular focus on \(v' {1}\) for which \. Learn how to change the basis of a subspace in r n and how to find the coordinates of a vector with respect to a basis. see examples, definitions, propositions and proofs. Learn how to convert a vector to a different basis and how to find the change of basis matrix. see examples, definitions, and proofs of the inverse property of change of basis matrices.
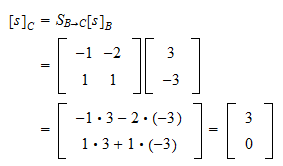
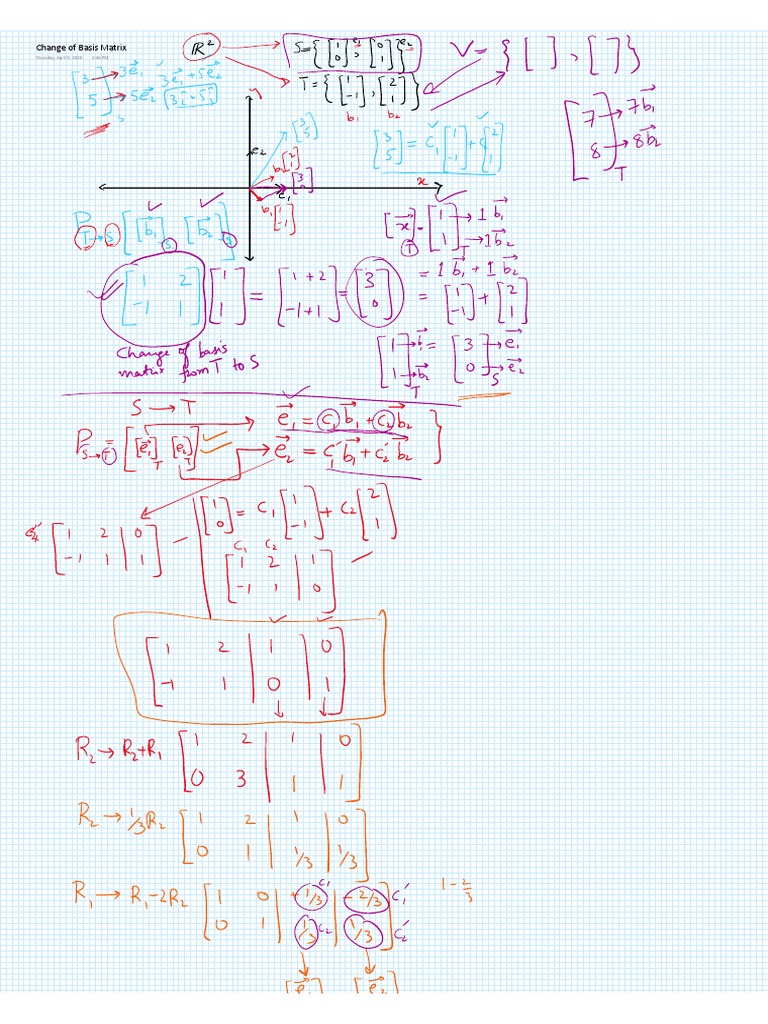
Change Of Basis Formula Examples Proofs Learn how to change the basis of a subspace in r n and how to find the coordinates of a vector with respect to a basis. see examples, definitions, propositions and proofs. Learn how to convert a vector to a different basis and how to find the change of basis matrix. see examples, definitions, and proofs of the inverse property of change of basis matrices. Change of basis in many applications, we may need to switch between two or more different bases for a vector space. so it would be helpful to have formulas for converting the components of a vector with respect to one basis into the corresponding components of the vector (or matrix of the operator) with respect to the other basis. This worksheet covers the concepts of change of coordinates matrix, similarity of matrices, and diagonalization of matrices in different bases. it contains problems and solutions related to linear transformations, vector spaces, and eigenvalues. Learn how to transform vectors and matrices using different bases and linear transformations. see examples, definitions and formulas for change of basis matrices and coordinates. In this tutorial, we will desribe the transformation of coordinates of vectors under a change of basis. we will focus on vectors in $r^2$, although all of this generalizes to $r^n$. the standard basis in $r^2$ is $ \left\{\left[{1 \atop 0} \right],\left[{0 \atop 1}\right]\right\}$.
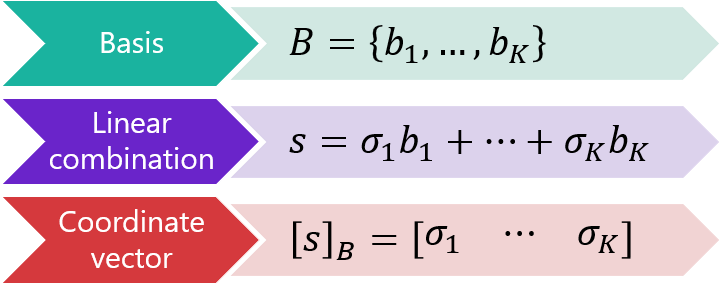
Change Of Basis Formula Examples Proofs Change of basis in many applications, we may need to switch between two or more different bases for a vector space. so it would be helpful to have formulas for converting the components of a vector with respect to one basis into the corresponding components of the vector (or matrix of the operator) with respect to the other basis. This worksheet covers the concepts of change of coordinates matrix, similarity of matrices, and diagonalization of matrices in different bases. it contains problems and solutions related to linear transformations, vector spaces, and eigenvalues. Learn how to transform vectors and matrices using different bases and linear transformations. see examples, definitions and formulas for change of basis matrices and coordinates. In this tutorial, we will desribe the transformation of coordinates of vectors under a change of basis. we will focus on vectors in $r^2$, although all of this generalizes to $r^n$. the standard basis in $r^2$ is $ \left\{\left[{1 \atop 0} \right],\left[{0 \atop 1}\right]\right\}$.
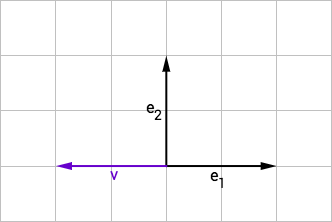
The Change Of Basis Matrix Learn how to transform vectors and matrices using different bases and linear transformations. see examples, definitions and formulas for change of basis matrices and coordinates. In this tutorial, we will desribe the transformation of coordinates of vectors under a change of basis. we will focus on vectors in $r^2$, although all of this generalizes to $r^n$. the standard basis in $r^2$ is $ \left\{\left[{1 \atop 0} \right],\left[{0 \atop 1}\right]\right\}$.
