
Permutation Groups Pdf Group Mathematics Permutation Chapter 5: permutation groups theorem 5.4 theorem: every element in s n is a product of 2 cycles. proof: since (a 1 a 2:::a k) = (a 1 a k)(a 1 a k 1) :::(a 1 a 3)(a 1 a 2); as you can check, any k cycle can be written as a product of 2 cycles. if ˙2s n is a product of two or more disjoint cycles, apply the above observation to each cycle, and. Chapter 5 permutation groups.pdf free download as pdf file (.pdf), text file (.txt) or read online for free. this document contains exercises about permutation groups. it defines some permutations σ, τ, and μ in s6 and asks the student to compute various products of these permutations.

Chapter 7 Permutations And Combination Pdf Numbers Permutation Math 403 chapter 5 permutation groups: 1. introduction: we now jump in some sense from the simplest type of group (a cylic group) to the most complicated. 2. de nition: given a set a, a permutation of ais a function f: a!awhich is 1 1 and onto. a permutation group of ais a set of permutations of athat forms a group under function composition. 3. In this chapter, we study certain groups of functions, called permutation groups, from a set a to itself. in the early and mid 19th century, groups of permutations were the only groups investigated by mathematicians. Permutation groups form one of the oldest parts of group theory. through the ubiquity of group actions and the concrete representations which they afford, both finite and infinite permutation groups arise in many parts of mathematics and continue to be a lively topic of research in their own right. 5.1 the structure of a permutation. the permutation group sn is the collection of all bijective maps σ : x → x of the set x = {1,2, ,n}, with composition of maps ( ) as the group operation. we introduced permutation groups in example 3.1.15 of section 3, which you should review before proceeding. there we introduced basic notation for.

Permutation Groups Department Of Mathematics At Kennesaw Permutation groups form one of the oldest parts of group theory. through the ubiquity of group actions and the concrete representations which they afford, both finite and infinite permutation groups arise in many parts of mathematics and continue to be a lively topic of research in their own right. 5.1 the structure of a permutation. the permutation group sn is the collection of all bijective maps σ : x → x of the set x = {1,2, ,n}, with composition of maps ( ) as the group operation. we introduced permutation groups in example 3.1.15 of section 3, which you should review before proceeding. there we introduced basic notation for. 5 permutation groups permutation groups are central to the study of geometric symmetries and to galois the ory, the study of finding solutions of polynomial equations. they also provide abundant examples of nonabelian groups. let us recall for a moment the symmetries of the equilateral triangle abc from chapter 3. Chapter 5 permutation groups. permutation groups are central to the study of geometric symmetries and to galois theory, the study of finding solutions of polynomial equations. they also provide abundant examples of nonabelian groups. let us recall for a moment the symmetries of the equilateral triangle \(\bigtriangleup abc\) from chapter 3. In this chapter, we construct some groups whose elements are called permutations. often, an action produced by a group element can be regarded as a function, and the binary operation of the.

Solved Every Permutation σ In S5 Is A Product Of Chegg 5 permutation groups permutation groups are central to the study of geometric symmetries and to galois the ory, the study of finding solutions of polynomial equations. they also provide abundant examples of nonabelian groups. let us recall for a moment the symmetries of the equilateral triangle abc from chapter 3. Chapter 5 permutation groups. permutation groups are central to the study of geometric symmetries and to galois theory, the study of finding solutions of polynomial equations. they also provide abundant examples of nonabelian groups. let us recall for a moment the symmetries of the equilateral triangle \(\bigtriangleup abc\) from chapter 3. In this chapter, we construct some groups whose elements are called permutations. often, an action produced by a group element can be regarded as a function, and the binary operation of the.
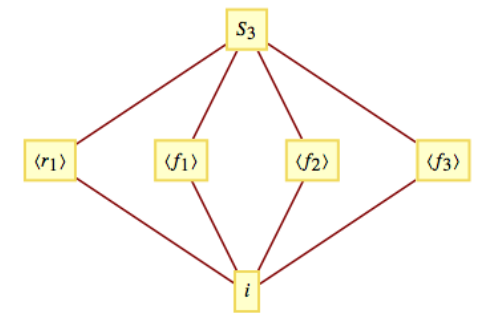
15 3 Permutation Groups Mathematics Libretexts In this chapter, we construct some groups whose elements are called permutations. often, an action produced by a group element can be regarded as a function, and the binary operation of the.
