
Solved Bã I 2 Cho Tam Giã C Abc Cã Ab Ac Gá I Am Lã Tia Phã N Cho 3 số dương 0 ≤ a ≤ b ≤ c ≤ 1. chứng minh a bc 1 b ac 1 c ab 1 ≤ 2 a b c 1 b a c 1 c a b 1 ≤ 2 . cho a là tập hợp các hình thoi, b là tập hợp các hình chữ nhật và c là tập hợp các hình vuông. khi đó: a. a ∩ b = c. b. a ∪ b = c. c. a \ b = c. với a, b, c là các số dương. Áp dụng bĐt am gm cho các số dương: \(a^2 bc\geq 2\sqrt{a^2bc}; b^2 ac\geq 2\sqrt{b^2ac}; c^2 ab\geq 2\sqrt{c^2ab}\) do đó: \(\text{vt}=\frac{1}{a^2 bc} \frac{1}{b^2 ac} \frac{1}{c^2 ab}\leq \frac{1}{2\sqrt{a^2bc}} \frac{1}{2\sqrt{b^2ac}} \frac{1}{2\sqrt{c hay.

Bài 1 Cho A B 2 B C 2 C A 2 A B 2c 2 B C A2a 2 C A 2b 2 Cho tam giác abc cân ở a và h là trung điểm bc.gọi i là hình chiếu vuông góc của h lên ac và o là trung điểm của hi. chứng minh a ) \(\widehat {aho} = \widehat {bci}\). Cho a, b, c >0 thỏa mãn: abc=1. cm: \(\dfrac{1}{a^2 ab b^2} \dfrac{1}{b^2 bc c^2} \dfrac{1}{c^2 ac a^2}\le a b c\). Cho a, b, c > 0. chứng minh (1 a^2 bc) (1 b^2 ac) (1 c^2 ab) >= (a b c) 2abc. cho a, b, c > 0 thỏa mãn (1 1 a) (1 1 b) (1 1 c) >= 2. Bài 1: cho a,b,c thỏa mãn (a b c) c=(b c a) a=(c a b) b tính p=(1 b a)*(1 c b)*(1 a c) bài 2: cho a b c=0 tính b=((a^2 b^2 c^2)*(b^2 c^2 a^2)*(c^2 a^2 b^2)) (10*a^2*b^2*c^2) bài 3: cho a^3*b^3 b^3*c^3 c^3*a^3=3*a^3*b^3*c^3 tính m(1 a b)*(1 b c)*(1 c a).

Solved Bã I 2 Cho Tam Giã C Nhá N Abc Cã ä æ á Ng Trã N O Cã ä æ Cho a, b, c > 0. chứng minh (1 a^2 bc) (1 b^2 ac) (1 c^2 ab) >= (a b c) 2abc. cho a, b, c > 0 thỏa mãn (1 1 a) (1 1 b) (1 1 c) >= 2. Bài 1: cho a,b,c thỏa mãn (a b c) c=(b c a) a=(c a b) b tính p=(1 b a)*(1 c b)*(1 a c) bài 2: cho a b c=0 tính b=((a^2 b^2 c^2)*(b^2 c^2 a^2)*(c^2 a^2 b^2)) (10*a^2*b^2*c^2) bài 3: cho a^3*b^3 b^3*c^3 c^3*a^3=3*a^3*b^3*c^3 tính m(1 a b)*(1 b c)*(1 c a). Cho đường tròn (o; r) và một điểm a sao cho oa = 2r, vẽ các tiếp tuyến ab, ac với (o; r), b và c là các tiếp điểm. vẽ đường kính bod. a) chứng minh 4 điểm a, b, o, c cùng thuộc một đường tròn. b) chứng minh rằng: dc oa. Khi đó từ \(ab bc ac=3\rightarrow ab\geq 1\) ta có bổ đề sau: với \(a,b>0,ab\geq 1\) thì \(\frac{1}{a^2 1} \frac{1}{b^2 1}\geq \frac{2}{ab 1}\) cách chứng minh bổ đề rất đơn giản, chỉ cần quy đồng ta có ngay đpcm quay trở lại bài. Đặt $(\frac{bc}{a^2},\frac{ca}{b^2},\frac{ab}{c^2})\rightarrow (x,y,z)$ thì xyz = 1 và ta cần chỉ ra rằng: $\frac{1}{2 x} \frac{1}{2 y} \frac{1}{2 z}\leqslant 1\leftrightarrow xyz xy yz zx 4\geqslant 0\leftrightarrow xy yz zx\geqslant 3$*đúng theo bất đẳng thức. Đáp án ` ` giải thích các bước giải: vì `a b c=0` nên: $\begin{cases} a b= c\\b c= a\\c a= b \end{cases}$ ``$\begin{cases} (a b)^2 =( c)^2\\(b c)^2 =( a)^2\\(c a)^2 =( b)^2 \end{cases}$ ``$\begin{cases} a^2 2ab b^2 =c^2 \\b^2 2bc c^2 =a^2 \\c^2 2ca a^2 =b.
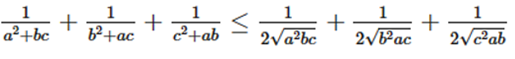
Cho A B C 0 Chá Ng Minh RẠNg 1 A 2 Bc 1 B 2 Ac 1 C 2 Ab Cho đường tròn (o; r) và một điểm a sao cho oa = 2r, vẽ các tiếp tuyến ab, ac với (o; r), b và c là các tiếp điểm. vẽ đường kính bod. a) chứng minh 4 điểm a, b, o, c cùng thuộc một đường tròn. b) chứng minh rằng: dc oa. Khi đó từ \(ab bc ac=3\rightarrow ab\geq 1\) ta có bổ đề sau: với \(a,b>0,ab\geq 1\) thì \(\frac{1}{a^2 1} \frac{1}{b^2 1}\geq \frac{2}{ab 1}\) cách chứng minh bổ đề rất đơn giản, chỉ cần quy đồng ta có ngay đpcm quay trở lại bài. Đặt $(\frac{bc}{a^2},\frac{ca}{b^2},\frac{ab}{c^2})\rightarrow (x,y,z)$ thì xyz = 1 và ta cần chỉ ra rằng: $\frac{1}{2 x} \frac{1}{2 y} \frac{1}{2 z}\leqslant 1\leftrightarrow xyz xy yz zx 4\geqslant 0\leftrightarrow xy yz zx\geqslant 3$*đúng theo bất đẳng thức. Đáp án ` ` giải thích các bước giải: vì `a b c=0` nên: $\begin{cases} a b= c\\b c= a\\c a= b \end{cases}$ ``$\begin{cases} (a b)^2 =( c)^2\\(b c)^2 =( a)^2\\(c a)^2 =( b)^2 \end{cases}$ ``$\begin{cases} a^2 2ab b^2 =c^2 \\b^2 2bc c^2 =a^2 \\c^2 2ca a^2 =b.

Cho A B C 0 Chá Ng Minh RẠNg 1 A 2 Bc 1 B 2 Ac 1 C 2 Ab Đặt $(\frac{bc}{a^2},\frac{ca}{b^2},\frac{ab}{c^2})\rightarrow (x,y,z)$ thì xyz = 1 và ta cần chỉ ra rằng: $\frac{1}{2 x} \frac{1}{2 y} \frac{1}{2 z}\leqslant 1\leftrightarrow xyz xy yz zx 4\geqslant 0\leftrightarrow xy yz zx\geqslant 3$*đúng theo bất đẳng thức. Đáp án ` ` giải thích các bước giải: vì `a b c=0` nên: $\begin{cases} a b= c\\b c= a\\c a= b \end{cases}$ ``$\begin{cases} (a b)^2 =( c)^2\\(b c)^2 =( a)^2\\(c a)^2 =( b)^2 \end{cases}$ ``$\begin{cases} a^2 2ab b^2 =c^2 \\b^2 2bc c^2 =a^2 \\c^2 2ca a^2 =b.

Cho A B C 0 Chá Ng Minh RẠNg A 3 A 2 B 2 B 3 B 2 C 2 C 3 C
