
Ab Bc Ca 0 Find 1 A2 Bc 1 B2 C1 C2 Ab 226307 A B C 2 Formula 1) cho a,b,c>0,ab bc ca=1. chứng minh rằng: a) s=a căn(1 a^2) b căn(1 b^2) c căn(1 c^2)<=3 2 b) p=1 a(a b) 1 b(b c) 1 c(c a)>=9 2 2) cho a,b,c>0,a b c=1. chứng minh rằng: i) a (b c)^2 b (c a)^2 c (a b)^2>=9 4 ii) bc căn(a bc) ca căn(b ca) ab. Không mất tính tổng quát, giả sử \(c=\min (a,b,c)\). khi đó từ \(ab bc ac=3\rightarrow ab\geq 1\) ta có bổ đề sau: với \(a,b>0,ab\geq 1\) thì \(\frac{1}{a^2 1} \frac{1}{b^2 1}\geq \frac{2}{ab 1}\) cách chứng minh bổ đề rất đơn giản, chỉ cần quy đồng ta có ngay.

Cho A B C 0 Và Ab Bc Ca 3 Cmr A 2b 3 1 B 2c 3 1 Cho tam giác abc có góc a = 2 lần góc b, góc b = 2 góc c. Đặt bc = a, ca =b, ab=c a> chứng minh bac > 90 và a^2 > b^2 c^2 b> chứng minh a^2 = b^2 bc và 1 a 1 b = 1 c. \(\frac{a}{1 b^2} \frac{b}{1 c^2} \frac{c}{1 a^2}\ge a b c \frac{ab bc c}{2}=3 \frac{ab bc ca}{2}\) mặt khác ,ta biết rằng \(ab bc ca\le\frac{\left(a b c\right)^2}{3}=3.\) từ đây ,kết hợp với đánh giá ở trên ,ta có kết quả cần chứng minh. Đáp án:. Qua a kẻ đường thẳng vuông góc với bd tại e, cắt cd tại i. qua c kẻ đường thẳng vuông góc với ab tại f, cắt ab tại k. a) tứ giác akci là hình gì? vì sao?.
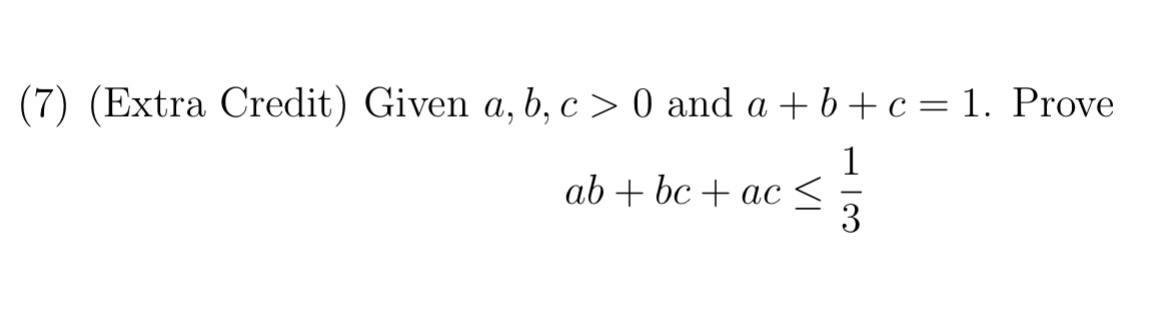
Solved Given A B C 0 And A B C 1 Prove Ab Bc Chegg Đáp án:. Qua a kẻ đường thẳng vuông góc với bd tại e, cắt cd tại i. qua c kẻ đường thẳng vuông góc với ab tại f, cắt ab tại k. a) tứ giác akci là hình gì? vì sao?. Giải thích các bước giải : `1 a 1 b 1 c=2` `(1 a 1 b 1 c)^2=2^2` `1 a^2 1 b^2 1 c^2 2 (ab) 2 (bc) 2 (ca)=4` `(1 a^2 1 b^2 1 c^2) 2(1 (ab) 1 (bc) 1 (ca))=4` vì `1 a^2 1 b^2 1 c^2=2` `2 2(1 (ab) 1 (bc) 1 (ca))=4` `2(1 (ab) 1 (bc) 1 (ca))=2` `1 (ab) 1 (bc) 1 (ca)=1. Cho a, b, c là các số dương. chứng minh bất đẳng thức: a) 2a (b c) (b c) 2a ≥ 2. b) a (b c) b (c a) c (a b) ≥ 3 2 (toán học lớp 8). Cho a,b,c khác 0 và 1 a 1 b 1 c=1 a b c. chứng minh 1 a n 1 b n 1 c n =1 (a b c) n (n thuộc n *,n lẻ) bài làm: ta có: \frac {1} {a} \frac {1} {b} \frac {1} {c}=\frac {1} {a b c} a1 b1 c1 = a b c1. \leftrightarrow\frac {ab bc ca} {abc}=\frac {1} {a b c} ⇔ abcab bc ca = a b c1. Cho tam giác abc có a (2 ; 6), b (– 2 ; 2), c (8 ; 0). khi đó, tam giác abc là: trong mặt phẳng toạ độ oxy, cho ba điểm a (1; 5), b (–1; –1), c (2; – 5). chứng minh ba điểm a, b, c không thẳng hàng. trong mặt phẳng toạ độ oxy, cho tam giác abc có a (– 2 ; 4), b (– 5 ; − 1), c (8 ; – 2).
Cho A B C 0 Vг Ab Bc Ca 1 Chб Ng Minh Rбє Ng S A в љ 1 A 2 Giải thích các bước giải : `1 a 1 b 1 c=2` `(1 a 1 b 1 c)^2=2^2` `1 a^2 1 b^2 1 c^2 2 (ab) 2 (bc) 2 (ca)=4` `(1 a^2 1 b^2 1 c^2) 2(1 (ab) 1 (bc) 1 (ca))=4` vì `1 a^2 1 b^2 1 c^2=2` `2 2(1 (ab) 1 (bc) 1 (ca))=4` `2(1 (ab) 1 (bc) 1 (ca))=2` `1 (ab) 1 (bc) 1 (ca)=1. Cho a, b, c là các số dương. chứng minh bất đẳng thức: a) 2a (b c) (b c) 2a ≥ 2. b) a (b c) b (c a) c (a b) ≥ 3 2 (toán học lớp 8). Cho a,b,c khác 0 và 1 a 1 b 1 c=1 a b c. chứng minh 1 a n 1 b n 1 c n =1 (a b c) n (n thuộc n *,n lẻ) bài làm: ta có: \frac {1} {a} \frac {1} {b} \frac {1} {c}=\frac {1} {a b c} a1 b1 c1 = a b c1. \leftrightarrow\frac {ab bc ca} {abc}=\frac {1} {a b c} ⇔ abcab bc ca = a b c1. Cho tam giác abc có a (2 ; 6), b (– 2 ; 2), c (8 ; 0). khi đó, tam giác abc là: trong mặt phẳng toạ độ oxy, cho ba điểm a (1; 5), b (–1; –1), c (2; – 5). chứng minh ba điểm a, b, c không thẳng hàng. trong mặt phẳng toạ độ oxy, cho tam giác abc có a (– 2 ; 4), b (– 5 ; − 1), c (8 ; – 2).

Cho A B C 0 Vг Ab Bc Ca 1 Chб Ng Minh Rбє Ng S A в љ 1 A 2 Cho a,b,c khác 0 và 1 a 1 b 1 c=1 a b c. chứng minh 1 a n 1 b n 1 c n =1 (a b c) n (n thuộc n *,n lẻ) bài làm: ta có: \frac {1} {a} \frac {1} {b} \frac {1} {c}=\frac {1} {a b c} a1 b1 c1 = a b c1. \leftrightarrow\frac {ab bc ca} {abc}=\frac {1} {a b c} ⇔ abcab bc ca = a b c1. Cho tam giác abc có a (2 ; 6), b (– 2 ; 2), c (8 ; 0). khi đó, tam giác abc là: trong mặt phẳng toạ độ oxy, cho ba điểm a (1; 5), b (–1; –1), c (2; – 5). chứng minh ba điểm a, b, c không thẳng hàng. trong mặt phẳng toạ độ oxy, cho tam giác abc có a (– 2 ; 4), b (– 5 ; − 1), c (8 ; – 2).

Cho A B C 0 Vг Ab Bc Ca 1 Chб Ng Minh Rбє Ng S A в љ 1 A 2
