Cho Hб Sau 1 Y Cдѓn Bгўc Hai X Y X 2 X Y 1 Cдѓn Bбє C Hai Y 1 Cho parabol (p): y = − 1 2 x 2 và đường thẳng (d): y = x 4. a. vẽ (p) và (d) trên cùng hệ trục tọa độ. b. tìm tọa độ giao điểm của (p) và (d) bằng phép tính. Cho hai hàm số: y = 3 2x^2 và y = x^2. vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng toạ độ trọn bộ lời giải sách bài tập toán 9 kết nối tri thức hay nhất giúp bạn làm bài tập trong sbt toán 9.
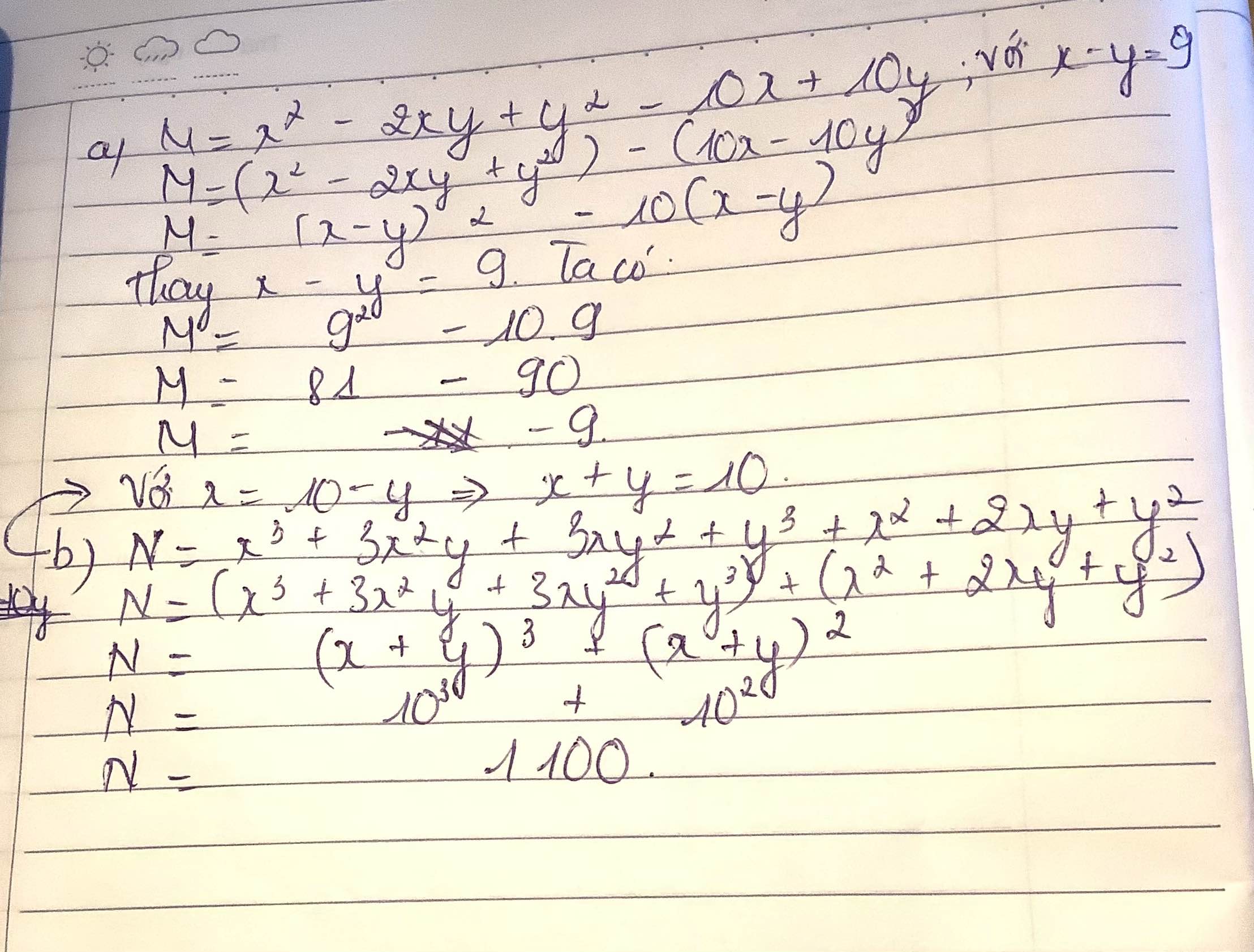
Phân Tích Các đa Thức Sau Thành Nhân Tử A X3 Y3 X Yb X3 Y3 X Yc X Y Cho hai hàm số bậc nhất : y=2x 5 và y =x 3 a) vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ . b) tìm tọa độ giao điểm của đồ thị trên . c) tìm m để đường thẳng y=3x m 3 đồng quy với đồ thị hai hàm số trên. Cho parabol (p):y=x^2 và đường thẳng d:y= 2x 3 a) vẽ (p) và (d) trên cùng 1 mặt phẳng toạ độ oxy b) tìm toạ độ giao điểm của (d) và (p) bằng phép toán c) gọi hoidap247 hỏi đáp online nhanh chóng, chính xác và luôn miễn phí. Cho hàm số \(y = {x^3} 2{x^2} \left( {m 1} \right)x 2m \). tìm \(m \) để từ điểm \(m \left( {1;2} \right) \) kẻ được 2 tiếp tuyến đến đồ thị. Cho hai hàm số \(y = {x^2}\) và \(y = 2x 3\). a) vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ. b) tìm tọa độ các giao điểm a và b của hai đồ thị đó. tính diện tích tam giác oab, với o là gốc tọa độ và đơn vị đo trên các trục tọa độ là xentimét.
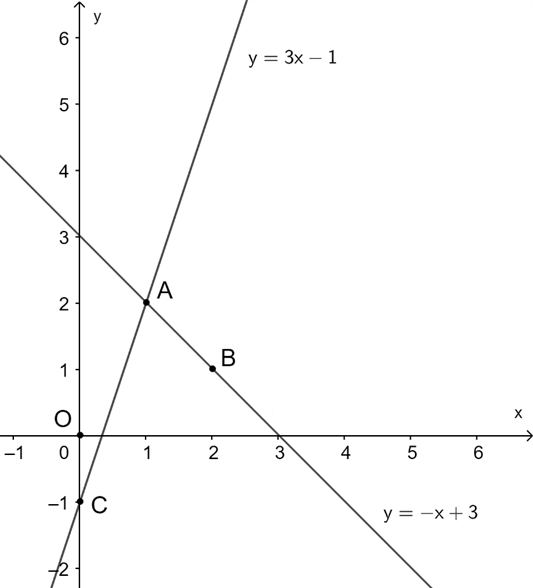
Cho Hai Hг M Sб Y в X 3 Vг Y 3x в 1 Cгі д б Thб Lбє N Lж б јt Lг Hai д ж б ќng Cho hàm số \(y = {x^3} 2{x^2} \left( {m 1} \right)x 2m \). tìm \(m \) để từ điểm \(m \left( {1;2} \right) \) kẻ được 2 tiếp tuyến đến đồ thị. Cho hai hàm số \(y = {x^2}\) và \(y = 2x 3\). a) vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ. b) tìm tọa độ các giao điểm a và b của hai đồ thị đó. tính diện tích tam giác oab, với o là gốc tọa độ và đơn vị đo trên các trục tọa độ là xentimét. Trong không gian với hệ trục oxyz, cho mặt phẳng (p): 2x y 2z 4 = 0, đường thẳng d: = = và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y z 4 = 0. viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (p) biết rằng tâm của mặt cầu có tọa. Cho hai hàm số y = 2x 3 và y = x 2 có đồ thị lần lượt là (d) và (p) 1 vẽ (d) và (p) trên cùng một hệ trục tọa độ oxy. 2 tìm tọa độ giao điểm của (d) và (p) bằng phép toán. Cho hàm số (p) : y = 1 2 x 2, đường thẳng (d) : y = 2x m 1 . 1) vẽ đồ thị hàm số (p) và (d) với m = 1 . 2) tìm giá trị của m để (d) cắt (p) tại hai điểm phân biệt. 3) tìm giá trị của m để (d) tiếp xúc với (p) . tìm tọa độ giao điểm . giải đúng mk tick . Vì `y = (3 a)x^2(a\ne3)` cắt đồ thị hàm số `y = x 3` tại điểm có hoành độ bằng ` 1` nên : `{(x= 1),((3 a)x^2 = x 3):}` `=> (3 a)*( 1)^2=( 1) 3` cho hàm số bậc hai y=(3−a)x, với giá trị nào của a thì đồ thị hàm số y=(3−a)x cắt đường thẳng y =x 3 tại điểm có hoành độ bằng.

Cho Hai Hàm Số Bậc Nhất Y M 1 X 2 Và Y 2m 3 X 3 M Tìm Giá Trị Trong không gian với hệ trục oxyz, cho mặt phẳng (p): 2x y 2z 4 = 0, đường thẳng d: = = và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y z 4 = 0. viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (p) biết rằng tâm của mặt cầu có tọa. Cho hai hàm số y = 2x 3 và y = x 2 có đồ thị lần lượt là (d) và (p) 1 vẽ (d) và (p) trên cùng một hệ trục tọa độ oxy. 2 tìm tọa độ giao điểm của (d) và (p) bằng phép toán. Cho hàm số (p) : y = 1 2 x 2, đường thẳng (d) : y = 2x m 1 . 1) vẽ đồ thị hàm số (p) và (d) với m = 1 . 2) tìm giá trị của m để (d) cắt (p) tại hai điểm phân biệt. 3) tìm giá trị của m để (d) tiếp xúc với (p) . tìm tọa độ giao điểm . giải đúng mk tick . Vì `y = (3 a)x^2(a\ne3)` cắt đồ thị hàm số `y = x 3` tại điểm có hoành độ bằng ` 1` nên : `{(x= 1),((3 a)x^2 = x 3):}` `=> (3 a)*( 1)^2=( 1) 3` cho hàm số bậc hai y=(3−a)x, với giá trị nào của a thì đồ thị hàm số y=(3−a)x cắt đường thẳng y =x 3 tại điểm có hoành độ bằng.
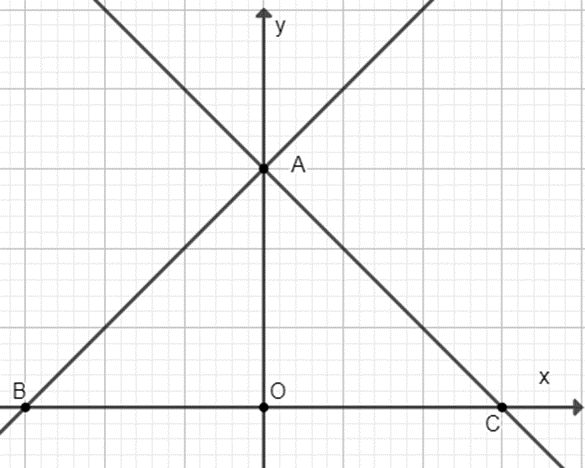
Cho Hai Hг M Sб Y X 3 Y в X 3 Cгі д б Thб Lбє N Lж б јt Lг Cгўc д ж б ќng Cho hàm số (p) : y = 1 2 x 2, đường thẳng (d) : y = 2x m 1 . 1) vẽ đồ thị hàm số (p) và (d) với m = 1 . 2) tìm giá trị của m để (d) cắt (p) tại hai điểm phân biệt. 3) tìm giá trị của m để (d) tiếp xúc với (p) . tìm tọa độ giao điểm . giải đúng mk tick . Vì `y = (3 a)x^2(a\ne3)` cắt đồ thị hàm số `y = x 3` tại điểm có hoành độ bằng ` 1` nên : `{(x= 1),((3 a)x^2 = x 3):}` `=> (3 a)*( 1)^2=( 1) 3` cho hàm số bậc hai y=(3−a)x, với giá trị nào của a thì đồ thị hàm số y=(3−a)x cắt đường thẳng y =x 3 tại điểm có hoành độ bằng.

Tг M M д б ѓ д б Thб Hг M Sб Y 2x 3 3 M 1 X 2 6mx M 3 Cгі Hai д Iб ѓm Cб C
