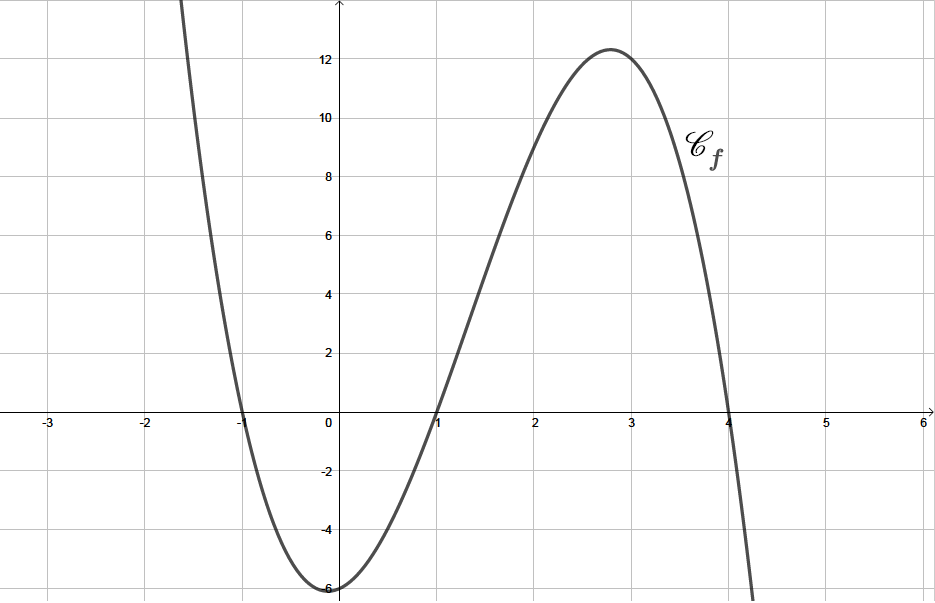
Comment Déterminer L Expression D Une Fonction Polynôme Du Troisième Connaitre l’expression algébrique d’une fonction polynôme du troisième degré. connaitre la représentation graphique des fonctions : x → ax3 et x → ax3 b. une fonction polynôme de degré 3 est une fonction f définie sur par f (x) = ax3 bx² cx d. Voici la méthode de résolution des polynômes du troisième degré recommandée en terminale. ne vous inquiétez pas, un exemple va suivre : on dispose donc d’un polynôme de degré 3 : f(x) = ax^3 bx^2 cx d; on cherche une racine évidente \alpha, on teste par exemple les valeurs 1, 1, 2, 2; on cherche ensuite k et l tels que ax^3.
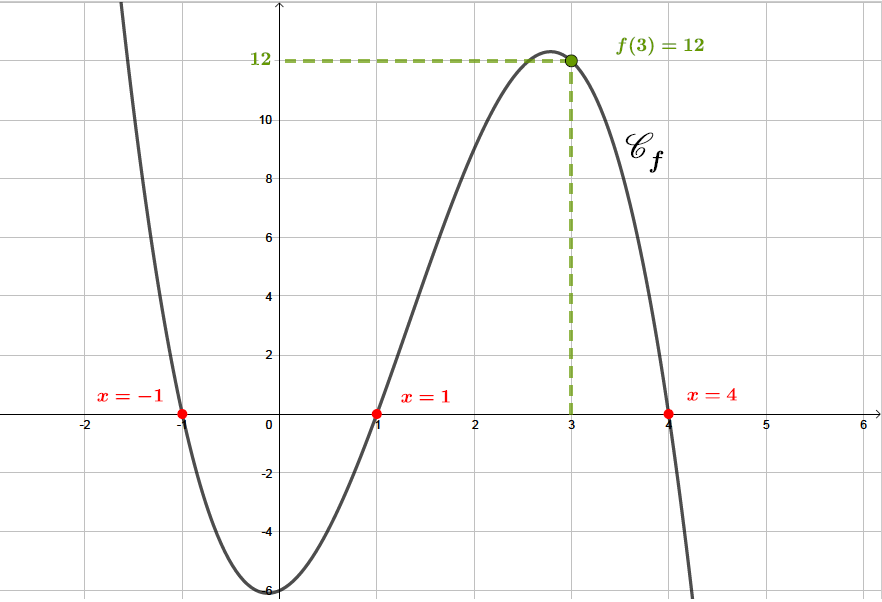
Comment Déterminer L Expression D Une Fonction Polynôme Du Troisième Une fonction polynomiale du troisième degré est une fonction qui peut s'exprimer sous la forme : : avec a, b, c et d quatre coefficients réels; a non nul. on parle de troisième degré car la puissance de x la plus élevée est 3. Soit f f une fonction polynôme de degré 3 3 dont la représentation graphique est donnée ci dessous. déterminer l'expression sous forme factorisée de f f . cette information va nous permettre de déterminer la valeur du réel. Factoriser, dans des cas simples, une expression du troisième degré connaissant au moins une de ses racines. utiliser la forme factorisée (en produit de facteurs du premier degré) d’un polynôme de degré 3 pour trouver ses racines et étudier son signe. résoudre une équation de la forme x3 = c, avec c > 0. La fonction ! définie par !(#)=5(#−4)(#−1)(# 3) est une fonction polynôme de degré 3 sous sa forme factorisée. si on développe l’expression de ! à l’aide d’un logiciel de calcul formel, on obtient bien.

Fonction Polynôme Du Troisième Degré Forum Mathématiques 473677 Factoriser, dans des cas simples, une expression du troisième degré connaissant au moins une de ses racines. utiliser la forme factorisée (en produit de facteurs du premier degré) d’un polynôme de degré 3 pour trouver ses racines et étudier son signe. résoudre une équation de la forme x3 = c, avec c > 0. La fonction ! définie par !(#)=5(#−4)(#−1)(# 3) est une fonction polynôme de degré 3 sous sa forme factorisée. si on développe l’expression de ! à l’aide d’un logiciel de calcul formel, on obtient bien. Soit f une fonction du troisième degré. on appelle racine de f, tout nombre x vérifiant f (x) = 0. une fonction du troisième degré admet au plus troisième racines distinctes dans r. combien de racines distinctes la fonction f: x ↦ x 3 − 1 possède t elle dans r? on a f (x) = 0 x 3 = 1. cette équation admet une unique solution : 3 1. ☺ une fonction polynôme de degré 3 est définie pour tout réel x par : f(x) = ax 3 bx 2 cx d a, b, c et d sont des nombres réels. déterminer l’expression de la fonction dérivée de cette fonction polynôme de degré 3. méthode : on décompose cette fonction en autant de fonction que l’on a de terme en x. f(x) = ax 3 bx. Exercice 2: Étude de fonction soit f une fonction polynôme du troisième degré de la forme : f(x) = x³ ax² 24x b, avec a et b des réels. on note & sa représentation graphique tracée dans le repère orthonormé ci dessous. 1. a) par lecture graphique, déterminer f(0) et f'(2).(f(0)= 16 et f’(2)=0. Une fonction polynôme du troisième degré est une fonction f définie sur par : f ( x ) = ax 3 bx 2 cx d où a, b , c et d sont quatre réels tels que a ≠ 0. exemples d'étude de fonction polynôme du troisième degré :.
