Les Identités Remarquables Leçon Apprentivore 🎯 tu veux la solution pour devenir solide en maths 💪 ? c'est ici 👉 hedacademy.frdans cette vidéo on apprend à utiliser les identités remarquabl. 📏 comprendre les identités remarquables (a b)² et (a b)² pour développer et factoriser facilement tes expressions algébriques ! 💡 dans cette vidéo, tu découvriras :.

Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Nous allons voir ici les pièges auxquels tu peux être confronté quand tu développes une identité remarquable. le premier piège, c’est de dire (a b) 2 = a 2 b 2 c’est évidemment totalement faux puisqu’il manque le 2ab !. Une identité remarquable est une équation qui tient vrai pour toutes valeurs substituées dans leurs variables. comprendre et connaître ces formules permet non seulement une méthode rapide pour effectuer des calculs complexes, mais facilite également une meilleure compréhension des concepts mathématiques fondamentaux pour la réussite des études. Les identités remarquables (3e) elles sont très utiles pour développer ou factoriser des expressions littérales rapidement. il faut les connaître dans les 2 sens. 1) carré d'une somme (a b)² = a² 2 × a × b b²; noté aussi : (a b)² = a² 2ab b². a² b² : somme des carrés. 2 × a × b ou 2ab : double produit. exemples. Dans ce cours, nous allons voir trois égalités qui permettent d'aller plus vite quand on fait du calcul littéral. ces égalités s'appellent les identités remarquables. l'égalité (a b)²=a² 2ab b² est la première identité remarquable. si a et b sont 2 nombres, nous pouvons développer (a b)² : vidéo de cours.

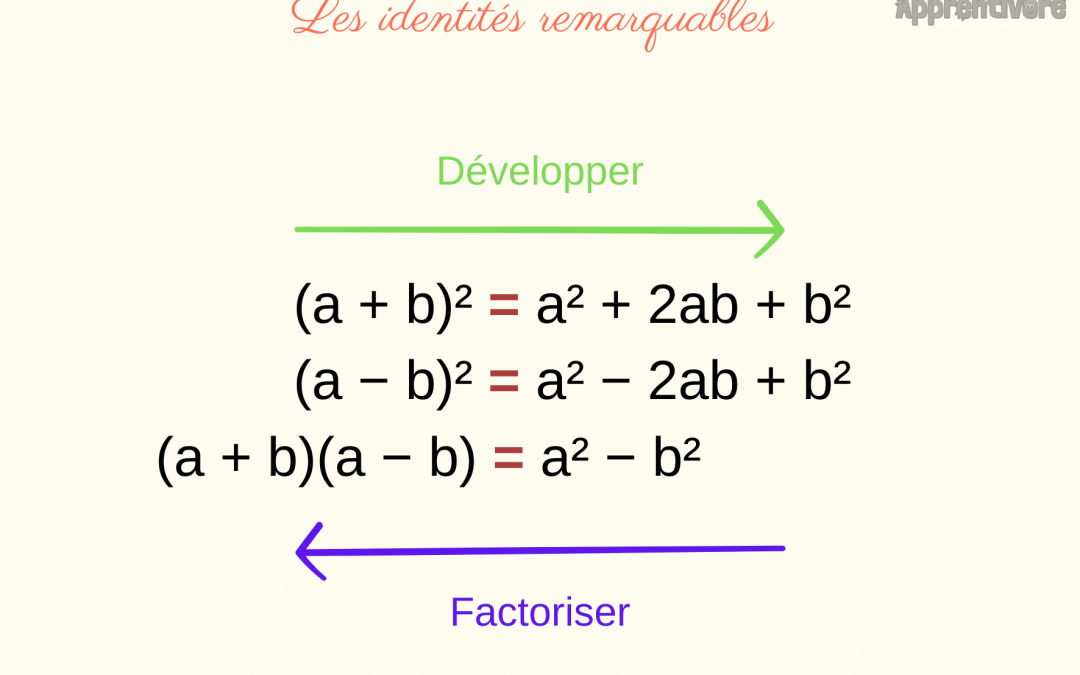
Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Les identités remarquables (3e) elles sont très utiles pour développer ou factoriser des expressions littérales rapidement. il faut les connaître dans les 2 sens. 1) carré d'une somme (a b)² = a² 2 × a × b b²; noté aussi : (a b)² = a² 2ab b². a² b² : somme des carrés. 2 × a × b ou 2ab : double produit. exemples. Dans ce cours, nous allons voir trois égalités qui permettent d'aller plus vite quand on fait du calcul littéral. ces égalités s'appellent les identités remarquables. l'égalité (a b)²=a² 2ab b² est la première identité remarquable. si a et b sont 2 nombres, nous pouvons développer (a b)² : vidéo de cours. Connaitre et savoir utiliser les identités remarquables pour développer et factoriser. Développer un produit, c'est l'écrire sous la forme d'une somme (ou d'une différence). propriétés : * ka kb = k (a b) * ka kb = k (a b) factoriser une somme (ou une différence), c'est l'écrire sous la forme d'un produit. propriétés des identités remarquables : (a b) ² = a² 2ab b² (a b) ² = a² 2ab b² (a b) (a b) = a² b². Comprendre l’utilisation des identités remarquables. on vous propose de développer et simplifier trois expressions algébriques en appliquant systématiquement les identités remarquables. l’objectif est de maîtriser le développement d’expressions et de mettre en évidence l’utilisation stratégique des identités suivantes. on. Les identités remarquables sont les expressions mathématiques qui sert à faire le calcul littéral. les identités remarquables sont utiles pour résoudre les équations. comment utilise t on ses identités remarquables ? comment développer ou factoriser une expression ? découvrez tout ce que vous devez savoir. 1. identités remarquables.

Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Connaitre et savoir utiliser les identités remarquables pour développer et factoriser. Développer un produit, c'est l'écrire sous la forme d'une somme (ou d'une différence). propriétés : * ka kb = k (a b) * ka kb = k (a b) factoriser une somme (ou une différence), c'est l'écrire sous la forme d'un produit. propriétés des identités remarquables : (a b) ² = a² 2ab b² (a b) ² = a² 2ab b² (a b) (a b) = a² b². Comprendre l’utilisation des identités remarquables. on vous propose de développer et simplifier trois expressions algébriques en appliquant systématiquement les identités remarquables. l’objectif est de maîtriser le développement d’expressions et de mettre en évidence l’utilisation stratégique des identités suivantes. on. Les identités remarquables sont les expressions mathématiques qui sert à faire le calcul littéral. les identités remarquables sont utiles pour résoudre les équations. comment utilise t on ses identités remarquables ? comment développer ou factoriser une expression ? découvrez tout ce que vous devez savoir. 1. identités remarquables.
