Living Across Borders In Conversation With Mohammad Chowdhury In geometry, $\cong$ means congruence of figures, which means the figures have the same shape and size. (in advanced geometry, it means one is the image of the other under a mapping known as an "isometry", which provides a formal definition of what "same shape and size" means) two congruent triangles look exactly the same, but they are not the. In mathematical notation, what are the usage differences between the various approximately equal signs "≈", "≃", and "≅"? the unicode standard lists all of them inside the mathematical operators b.
Arjun Chowdhury And The Myth Of International Order Department Of This approach uses the chinese remainder lemma and it illustrates the "unique factorization of ideals" into products of powers of maximal ideals in dedekind domains: it follows $ 1 \cong 10 1 \cong 9$ hence you get a well defined map $$\phi: \mathbb {z} [i] \rightarrow b$$ by defining $\phi (a bi):=a 3b$. Let $r$ be a ring with unity, and let $e$ be an idempotent element of $r$ such that $e^2 = e$. if $e$ is a central idempotent of $r$, then we obtain the following ring isomorphism: $$ r rer \cong (. I went through several pages on the web, each of which asserts that $\operatorname {aut} a n \cong \operatorname {aut} s n \; (n\geq 4)$ or an equivalent statement without proof, and many of them seem to regard it as a trivial fact. Are you sure that $\left\ {\pmatrix { a & b\\0&a^2}\mid a,b\in k, a\ne 0\right\}\cong (k, )$?.
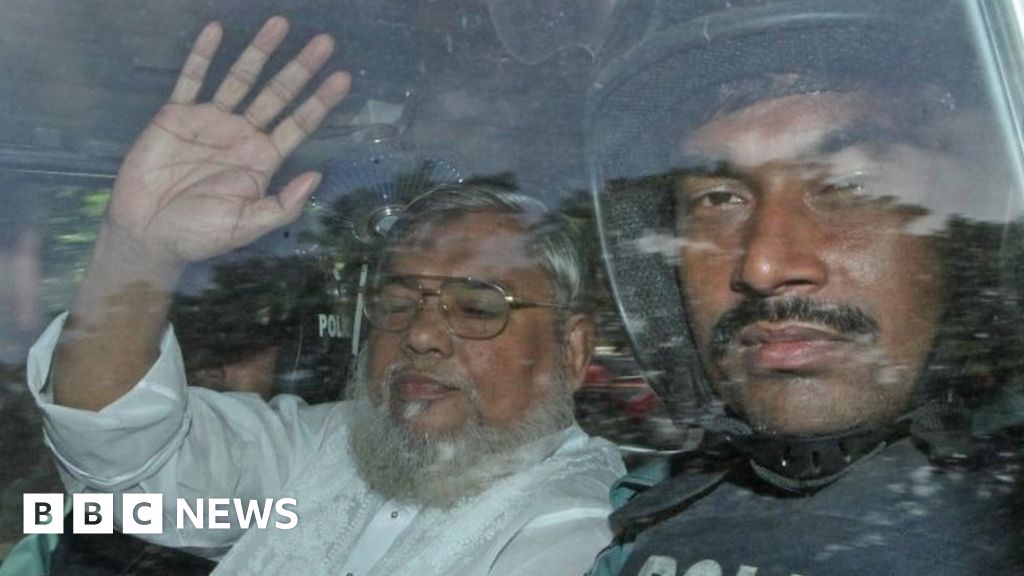
Bangladesh Hangs Chowdhury And Mujahid Over 1971 War Crimes Bbc News I went through several pages on the web, each of which asserts that $\operatorname {aut} a n \cong \operatorname {aut} s n \; (n\geq 4)$ or an equivalent statement without proof, and many of them seem to regard it as a trivial fact. Are you sure that $\left\ {\pmatrix { a & b\\0&a^2}\mid a,b\in k, a\ne 0\right\}\cong (k, )$?. Originally you asked for $\mathbb {z} (m) \otimes \mathbb {z} (n) \cong \mathbb {z} \text {gcd} (m,n)$, so any old isomorphism would do, but your proof above actually shows that $\mathbb {z} \text {gcd} (m,n)$ $\textit {is}$ the tensor product. Continue to help good content that is interesting, well researched, and useful, rise to the top! to gain full voting privileges,. Let $g$ be a group with some completely reducible finite dimensional representations $v,w$, and let $\\mathbf{1}$ be the trivial irreducible representation. i'm. A symbol i have in my math homework looks like a ~ above a =. (that is, $\\cong$.) what does this mean? i'm studying congruency at the moment if that helps.
Comments are closed.