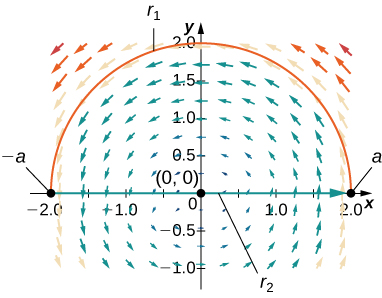
5 4e Conservative Vector Fields Exercises Mathematics Libretexts Let →f = p →i q→j f → = p i → q j → be a vector field on an open and simply connected region d d. then if p p and q q have continuous first order partial derivatives in d d and ∂p ∂y = ∂q ∂x ∂ p ∂ y = ∂ q ∂ x the vector field →f f → is conservative. We examine the fundamental theorem for line integrals, which is a useful generalization of the fundamental theorem of calculus to line integrals of conservative vector fields. we also discover show how to test whether a given vector field is conservative, and determine how to build a potential function for a vector field known to be conservative.

Conservative Vector Fields Math 275 Studocu In vector calculus, a conservative vector field is a vector field that is the gradient of some function. [1] a conservative vector field has the property that its line integral is path independent; the choice of path between two points does not change the value of the line integral. Let f = mi^ nj^ pk^ f = m i ^ n j ^ p k ^ be a vector field whose components are continuous throughout an open connected region d in space. then f is conservative if and only it f is a gradient field f f for a differentiable function f. Explain how to find a potential function for a conservative vector field. use the fundamental theorem for line integrals to evaluate a line integral in a vector field. explain how to test a vector field to determine whether it is conservative. In vector calculus, a conservative vector field is a vector field that is the gradient of some function. a conservative vector field has the property that its line integral is path independent.
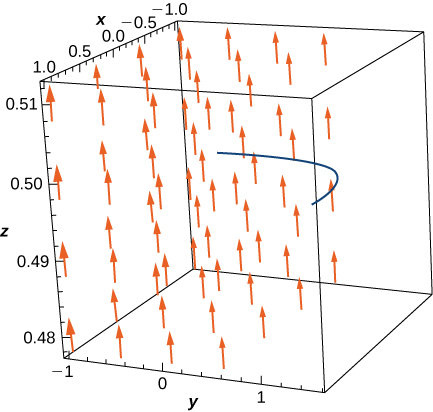
15 3e Conservative Vector Fields Exercises Mathematics Libretexts Explain how to find a potential function for a conservative vector field. use the fundamental theorem for line integrals to evaluate a line integral in a vector field. explain how to test a vector field to determine whether it is conservative. In vector calculus, a conservative vector field is a vector field that is the gradient of some function. a conservative vector field has the property that its line integral is path independent. One important class of vector fields that are relatively easy to work with, at least sometimes, but that still arise in many applications are “conservative vector fields”. the vector field ⇀ f is said to be conservative if there exists a function φ such that ⇀ f = ⇀ ∇φ. · dr = ∇f(r(t)) · dt = f(r(t)) dt. t=a dt t=a dt by the fundamental theorem of calculus, this is equal to f(r(b)) − f(r(a)) = f(b) − f(a). at gradient fields are always conservative, but the reverse is also always true. whenever a vector field is conservative, t ere is only one explanation: it is the gradient field of some scalar function. Conservative fields are independent of path. the line integral of a conservative field depends only on the value of the potential function at the endpoints of the domain curve. given vector field f f, we can test whether f f is conservative by using the cross partial property. We also discover show how to test whether a given vector field is conservative, and determine how to build a potential function for a vector field known to be conservative.
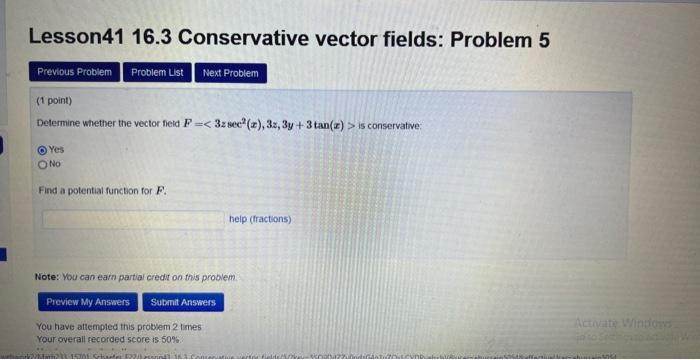
Solved Conservative Vector Fields Lesson4116 3 Conservati One important class of vector fields that are relatively easy to work with, at least sometimes, but that still arise in many applications are “conservative vector fields”. the vector field ⇀ f is said to be conservative if there exists a function φ such that ⇀ f = ⇀ ∇φ. · dr = ∇f(r(t)) · dt = f(r(t)) dt. t=a dt t=a dt by the fundamental theorem of calculus, this is equal to f(r(b)) − f(r(a)) = f(b) − f(a). at gradient fields are always conservative, but the reverse is also always true. whenever a vector field is conservative, t ere is only one explanation: it is the gradient field of some scalar function. Conservative fields are independent of path. the line integral of a conservative field depends only on the value of the potential function at the endpoints of the domain curve. given vector field f f, we can test whether f f is conservative by using the cross partial property. We also discover show how to test whether a given vector field is conservative, and determine how to build a potential function for a vector field known to be conservative.

Solved 4 Conservative Vector Fields Consider The Vector Chegg Conservative fields are independent of path. the line integral of a conservative field depends only on the value of the potential function at the endpoints of the domain curve. given vector field f f, we can test whether f f is conservative by using the cross partial property. We also discover show how to test whether a given vector field is conservative, and determine how to build a potential function for a vector field known to be conservative.
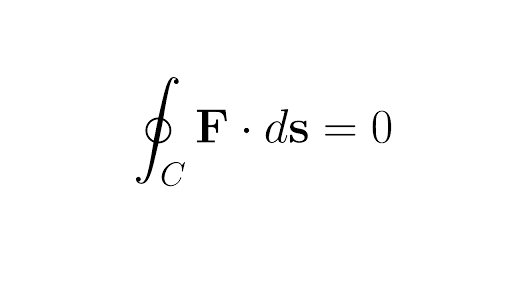
Conservative Vector Fields Article Khan Academy
