
Solved Q4 Consider The Following Bivariate Cdf Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: q4. consider the following bivariate cdf: fx1,x2 (x1,x2)= [1−e−x1−e−x2 e−x12 x22]i [0,∞) (x1)i [0,∞) (x2). (10 10=20 points ) find expressions for (a) the bivariate pdf and (b) the marginal pdfs. there’s just one step to solve this. q4. ***** problem statement *****consider the following bivariate cdf: ***** about altequal *****altequal is.

2 Consider The Following Bivariate Cdffx Y X Y Chegg Consider two discrete random variables x and y whose values are r and s respectively and suppose that the probability of the event {x = r}∩{y = s} is given by: p(x = r,y = s) = r s 48, if 0 6 r,s 6 3 0, otherwise the probabilities may be tabulated thus: y s → 0 1 2 3 x 0 0 48 1 48 2 48 3 48 6 48 1 1 48 2 48 3 48 4 48 10 48 p(x = r) r 2 2. Is there any way to recover a "closed form expression" for the cdf of a bivariate normal distribution? what i have in mind is the following: for a univariate standard normal, we can write. pr(x ≤ x) = 1 2(1 erf(x 2–√)) pr (x ≤ x) = 1 2 (1 erf (x 2)) in terms of the error function. ### solution by steps ***step 1: check if it's a valid density function*** to check if the given function is a valid density function, we need to ensure that it is non negative and integrates to 1 over its entire domain. \ [ \int {0}^ {1} \int {0}^ {1} \frac {12} {7}\left (x^ {2} x y\right) dx dy \] integrating first with respect to \ (x\):. Do not assume that x is a binomial random variable. let f(u) denote the cdf of x. (a)express the probability that the newsboy is able to sell all h papers in terms of f(u). solution: the newsboy sells all his papers if and only if the demand is h or more, i.e., if and only if the event fx hgoccurs. pfx hg= 1 pfx h 1g= 1 f(h 1).
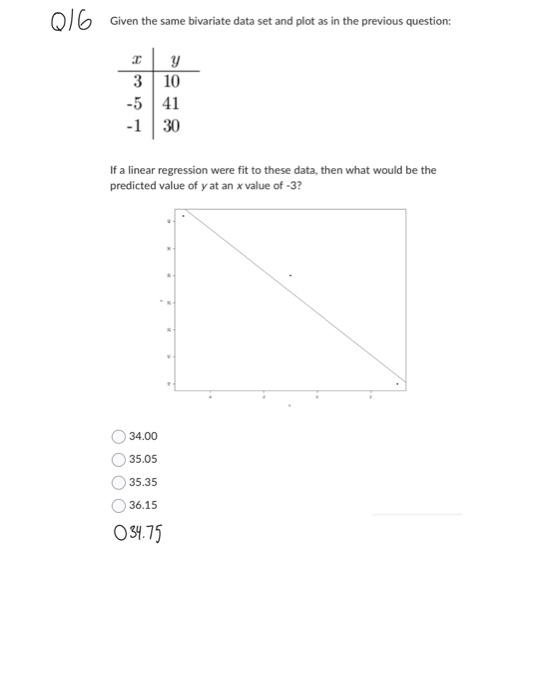
Solved Consider The Following Bivariate Data Set The Chegg ### solution by steps ***step 1: check if it's a valid density function*** to check if the given function is a valid density function, we need to ensure that it is non negative and integrates to 1 over its entire domain. \ [ \int {0}^ {1} \int {0}^ {1} \frac {12} {7}\left (x^ {2} x y\right) dx dy \] integrating first with respect to \ (x\):. Do not assume that x is a binomial random variable. let f(u) denote the cdf of x. (a)express the probability that the newsboy is able to sell all h papers in terms of f(u). solution: the newsboy sells all his papers if and only if the demand is h or more, i.e., if and only if the event fx hgoccurs. pfx hg= 1 pfx h 1g= 1 f(h 1). Input: these are only first 20 rows of the data points. input has 1000s of rows and of which col[1] and col[3] needs to be plotted as they posses a user and keyword frequency relationship. code: univeriate dataset. i am looking for some option for bivariate data points. The following are a number of practice problems that may be . helpful. for completing the homework, and will likely be . very useful. for studying for exams. 1. consider two continuous random variables x and y with joint p.d.f. f (x, y) =. To convince ourselves that f(x, y) is a valid cdf, we show that for all x y , hence, fx(x)fy (y) is a valid joint cdf. which completes the proof of the theorem. first, we find the cdf fx(x) and fy (y). x y thus, we have the contradiction that e−( ) 0 for all x, y 0. we can conclude that the given. function is not a valid cdf. thus c = 1 28. Definition: a random variable x that can (theoretically) assume any value in a finite or infinite interval is said to be continuous. the depth measurement of a lake, the life time of a component and the height of students in a class are some examples of continuous rvs. what is probability density function?.
