
Basis Vectors In Linear Algebra Ml Geeksforgeeks Given the basis $\beta = \{(1, 1,3),( 3,4,9),(2, 2,4)\}$ and $x = (8, 9, 6)$, i am to find the corresponding coordinate vector $[x] \beta$. i claim that the coordinate vectors entries $x 1,x 2,x 3$ meet the following criterion:. In this section, we interpret a basis of a subspace v v as a coordinate system on v v, and we learn how to write a vector in v v in that coordinate system. if b = {v1, v2, ⋯,vm} b = {v 1, v 2, ⋯, v m} is a basis for a subspace v v, then any vector x x in v v can be written as a linear combination.
Solved Find The Coordinate Vector X Of X Relative To The Given In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers (a tuple) that describes the vector in terms of a particular ordered basis. [1] an easy example may be a position such as (5, 2, 1) in a 3 dimensional cartesian coordinate system with the basis as the axes of this system. Use coordinate vectors to determine if fp1; p2; p3g is a linearly independent set: p1 = 1 t, p2 = 2 t t2, p3 = 2t 3t2. = 1; t; t2 . by the imt, [p1] ; [p2] ; [p3] is linearly therefore fp1; p2; p3g is linearly . coordinate vectors also allow us to associate vector spaces with subspaces of other vectors spaces. let h =spanfb1; b2g. The coordinates \(\{{\mathbf x}\} {\mathcal{b}}\) are the weights that form \(\mathbf x\) as a linear combination of basis vectors. if the basis vectors form the columns of the matrix \(c {\mathcal{b}}\text{,}\) then \(\{{\mathbf x}\} {\mathcal{b}} = c {\mathcal{b}}\mathbf x\text{.}\). In this video i provide a conceptual understanding of coordinate vectors relative to a basis then go into the process of finding coordinate vectors relative to a basis in normal.
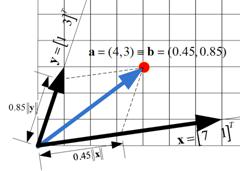
Linear Algebra Tutorial Basis Vector The coordinates \(\{{\mathbf x}\} {\mathcal{b}}\) are the weights that form \(\mathbf x\) as a linear combination of basis vectors. if the basis vectors form the columns of the matrix \(c {\mathcal{b}}\text{,}\) then \(\{{\mathbf x}\} {\mathcal{b}} = c {\mathcal{b}}\mathbf x\text{.}\). In this video i provide a conceptual understanding of coordinate vectors relative to a basis then go into the process of finding coordinate vectors relative to a basis in normal. The column vector \([v] e\) is called the coordinate vector of \(v\) with respect to the basis \(e\). example \(\pageindex{1}\): recall that the vector space \(\mathbb{r} 1[x]\) of polynomials over \(\mathbb{r}\) of degree at most 1 is an inner product space with inner product defined by. Let v be a finite dimensional vector space. [x]b is also known as the b coordinate vector of x. c1; c2; : : : ; cn are also known as the b coordinates of x. the order of the vectors in the basis is critical, hence the term ordered basis. recall the standard bases for common vector spaces: dim. We begin with a vector space v that has a basis b = {v1, . . ., vn}. we always keep the same order for vectors in the basis. technically, this is called an ordered basis. if v ∈ v , then we can always express v ∈ v in exactly one way as a linear combination of the the vectors in b. Courses on khan academy are always 100% free. start practicing—and saving your progress—now: khanacademy.org math linear algebra alternate bases.
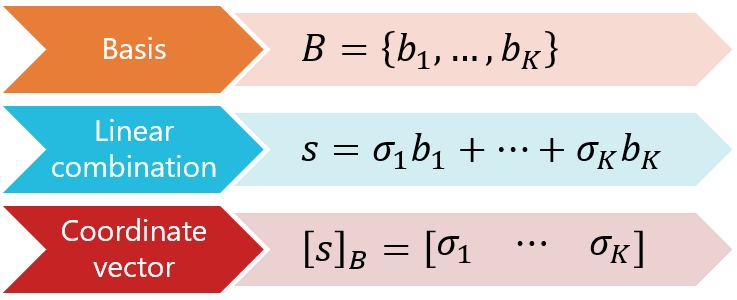
Coordinate Vector The column vector \([v] e\) is called the coordinate vector of \(v\) with respect to the basis \(e\). example \(\pageindex{1}\): recall that the vector space \(\mathbb{r} 1[x]\) of polynomials over \(\mathbb{r}\) of degree at most 1 is an inner product space with inner product defined by. Let v be a finite dimensional vector space. [x]b is also known as the b coordinate vector of x. c1; c2; : : : ; cn are also known as the b coordinates of x. the order of the vectors in the basis is critical, hence the term ordered basis. recall the standard bases for common vector spaces: dim. We begin with a vector space v that has a basis b = {v1, . . ., vn}. we always keep the same order for vectors in the basis. technically, this is called an ordered basis. if v ∈ v , then we can always express v ∈ v in exactly one way as a linear combination of the the vectors in b. Courses on khan academy are always 100% free. start practicing—and saving your progress—now: khanacademy.org math linear algebra alternate bases.
