Vector Algebra Vector And Coordinate Geometry In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers (a tuple) that describes the vector in terms of a particular ordered basis. [1] an easy example may be a position such as (5, 2, 1) in a 3 dimensional cartesian coordinate system with the basis as the axes of this system. Coordinate vectors. this is a brief discussion of coordinate vectors and the notation for them that i presented in class. here is the setup for all of the problems. we begin with a vector space vthat has a basis b= fv 1;:::;v ng { i.e., a spanning set that is linearly independent. we always keep the same order for vectors in the basis.
Vector Algebra Vector And Coordinate Geometry Explain the connection between polar coordinates and cartesian coordinates in a plane. vectors are usually described in terms of their components in a coordinate system. even in everyday life we naturally invoke the concept of vector components in a rectangular coordinate system. There are three commonly used coordinate systems: cartesian, cylindrical and spherical. in this chapter we will describe a cartesian coordinate system and a cylindrical coordinate system. 3.2.1 cartesian coordinate system . cartesian coordinates consist of a set of mutually perpendicular axes, which intersect at a. When we express a vector in a coordinate system, we identify a vector with a list of numbers, called coordinates or components, that specify the geometry of the vector in terms of the coordinate system. here we will discuss the standard cartesian coordinate systems in the plane and in three dimensional space. Discover how coordinate vectors can be used to represent the elements of an abstract linear space, with proofs, examples and solved exercises.

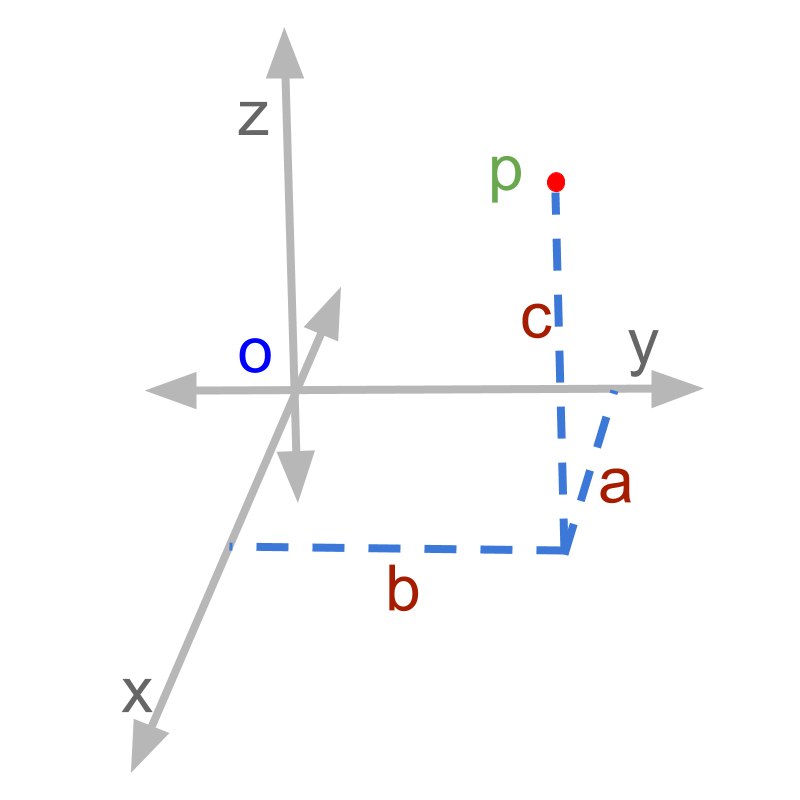
Vectors In Two And Three Dimensional Cartesian Coordinates Math Insight When we express a vector in a coordinate system, we identify a vector with a list of numbers, called coordinates or components, that specify the geometry of the vector in terms of the coordinate system. here we will discuss the standard cartesian coordinate systems in the plane and in three dimensional space. Discover how coordinate vectors can be used to represent the elements of an abstract linear space, with proofs, examples and solved exercises. Coordinate vectors the commonest way to establish an invertible linear trans formation (i.e. linear isomorphism) between rn and a general n dimensional vector space v is to choose a basis b = fb 1;b 2;:::;b ngof v. then we de ne the linear transformation l b:rn!v by l b(k 1;k 2;:::;k n) = k 1b 1 k 2b 2 ::: k nb n in v. (4) so l b(e i) = b. Vector can be expressed in a particular coordinate system by an ordered list of numbers, which are called the “components” of the vector. the components have meaning only with respect to the particular coordinate system. The coordinate vector of the polynomial \(p(x)=3x 2\in \mathbb{r} 1[x]\) is, e.g., \[ [p(x)] e= \frac{1}{2} \begin{bmatrix} 7 \\ \sqrt{3} \end{bmatrix}. note also that the map \([\,\cdot\,] e\) is an isomorphism (meaning that it is an injective and surjective linear map) and that it is also inner product preserving. The xj’s are the coordinates of v relative to b. we collect them into the coordinate vector [v]b = x1 xn . examples. here are some examples. let v = p2 and b = {1,x,x2}. what is the coordinate vector [5 3x− x2]b? answer: [5 3x− x2]b = 5 3 −1 . if we ask the same question for [5 − x2 3x]b, the answer is the same, because to find.
