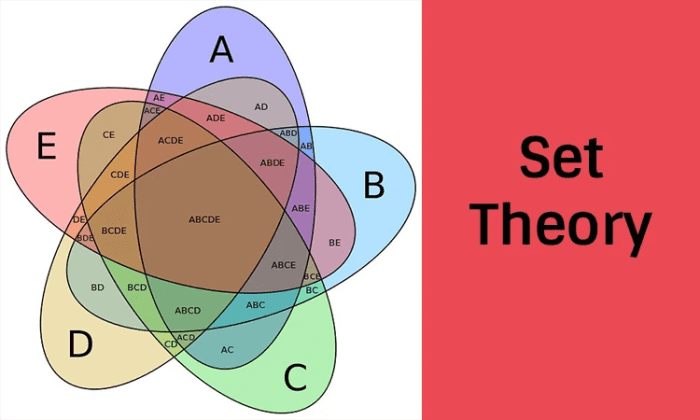
Set Theory In Discrete Mathematics Owlcation Let x ∈ a∩bc. by definition of intersection, x ∈ a and x ∈ bc. by definition of complement, x ∈ bc implies that x 6∈b. hence, x ∈ a and x 6∈b. by definition of set difference, x ∈ a− b. thus, a−b = a∩bc. here are some basic subset proofs about set operations. theorem for any sets a and b, a∩b ⊆ a. proof: let x. This workbook covers a number of topics in discrete mathematics with particular emphasis on basic concepts and their logic. it does not replace the textbook, and is not intended for independent study. instead it presents basic concepts, definitions, examples and exercises to be studied in class, individually and in groups.
Solved Discrete Mathematics Logic Set Theory Proof A Chegg Let \ (a\) be a subset of a universal set \ (u\) and let \ (u\in u\text {.}\) to use this method we note that exactly one of the following is true: \ (u \in a\) or \ (u\notin a\text {.}\) denote the situation where \ (u \in a\) by 1 and that where \ (u \notin a\) by 0. Try out a few examples. find a pattern. every odd integer is equal to the difference between the squares of two integers. any odd integer can be written as (2k 1) for some integer k. we rewrite the expression as follows. Example a proposition fp : p is a prime numberg\fk2 1 : k 2ng= f3g. proof. let x 2fp : p is a prime numberg\fk2 1 : k 2ng so that x is prime and x = k2 1 = (k 1)(k 1). this shows that x has two factors. every prime number has two positive factors 1 and itself, so either (k 1) = 1 or (k 1) = 1. since these factors must be positive we know. How to prove that one set is a subset of the other: the element argument given sets x and y, the following shows that x y. (1) let x be an element of x. (2) prove that x is an element of y. (3) conclude that x y. example: let a and b be the following sets, a = fm 2zjm = 6r 12 for some r 2zg b = fm 2zjm = 3s for some s 2zg (1) prove that a b.

Solved A Set Theory Discrete Mathematics I Let A B C Chegg Example a proposition fp : p is a prime numberg\fk2 1 : k 2ng= f3g. proof. let x 2fp : p is a prime numberg\fk2 1 : k 2ng so that x is prime and x = k2 1 = (k 1)(k 1). this shows that x has two factors. every prime number has two positive factors 1 and itself, so either (k 1) = 1 or (k 1) = 1. since these factors must be positive we know. How to prove that one set is a subset of the other: the element argument given sets x and y, the following shows that x y. (1) let x be an element of x. (2) prove that x is an element of y. (3) conclude that x y. example: let a and b be the following sets, a = fm 2zjm = 6r 12 for some r 2zg b = fm 2zjm = 3s for some s 2zg (1) prove that a b. Def: a proof by cases uses the following rule of inference: p → r premise 1 q → r premise 2 p ∨ q premise 3 r conclusion example 1.5.7: a theorem let x be any integer. then x2 x is even. proof: setup for proof by cases inference p : x is even; q : x is odd; r : x2 x is even. verify premise 1. if x is even, then x = 2n, for some integer n. In the first paragraph, we set up a proof that a ⊆ d ∪ e by picking an arbitrary x ∈ a. in the second, we used the fact that a ⊆ b ∪ c to conclude that x ∈ b ∪ c. proving that one set is a subset of another introduces a new variable; using the fact that one set is a subset of the other lets us conclude new things about existing.

Set Proof Examples Notes A âš B â ì B âš ì A Show That For A And B Def: a proof by cases uses the following rule of inference: p → r premise 1 q → r premise 2 p ∨ q premise 3 r conclusion example 1.5.7: a theorem let x be any integer. then x2 x is even. proof: setup for proof by cases inference p : x is even; q : x is odd; r : x2 x is even. verify premise 1. if x is even, then x = 2n, for some integer n. In the first paragraph, we set up a proof that a ⊆ d ∪ e by picking an arbitrary x ∈ a. in the second, we used the fact that a ⊆ b ∪ c to conclude that x ∈ b ∪ c. proving that one set is a subset of another introduces a new variable; using the fact that one set is a subset of the other lets us conclude new things about existing.

Discrete Mathematics And Proof 34 Examples Let U Be A Set And Let A

Solution Discrete Mathematics Set Theory Studypool
