
Evaluating A B From A Proportion In Two Ways Cool Math Tricks ⭐ join this channel to get access to perks:→ bit.ly 3cbgfr1 my merch → teespring stores sybermath?page=1follow me → twitter s. It can be written in two ways: as two equal fractions a b = c d; or using a colon, a:b = c:d. the following proportion is read as "twenty is to twenty five as four is to five." in problems involving proportions, we can use cross products to test whether two ratios are equal and form a proportion.
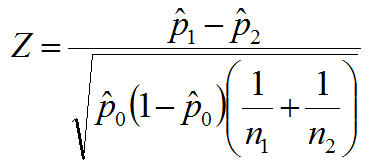
Two Sample Proportion Test With Minitab Lean Sigma Corporation There are many formulae that can apply to proportions, but the basic starting point is a b = c d. going from there, you can get a variety of other formulae, such as a x d = b x c and b^2 = a x c. It is easy to calculate if ratios are proportional. to check if the ratio a: b and c: d is proportional. continued proportion. two ratios a: b and b: c is said to be in continued proportion if a: b = b: c. in this case, the term c is called the third proportion of a and b whereas b is called the mean proportion of between the terms a and c. Reducing the ratios to lowest terms, we obtain the ratio of a : b as 1 : 2 and the ratio of c : d as 1 : 2. since these ratios are equivalent, they are proportional to each other, and their proportion equation is: a: b = c: d. the proportion equation can also be formed by representing the ratios as fractions. Determine if a proportion is true: you can tell if a simple proportion is true by looking at each of the ratios (fractions). if the fractions both reduce to the same value, the proportion is true.

Solved Test And Ci For Two Proportion A B Difference Chegg Reducing the ratios to lowest terms, we obtain the ratio of a : b as 1 : 2 and the ratio of c : d as 1 : 2. since these ratios are equivalent, they are proportional to each other, and their proportion equation is: a: b = c: d. the proportion equation can also be formed by representing the ratios as fractions. Determine if a proportion is true: you can tell if a simple proportion is true by looking at each of the ratios (fractions). if the fractions both reduce to the same value, the proportion is true. A proportion is a name we give to a statement that two ratios are equal. it can be written in two ways: two equal fractions, or, using a colon, a:b = c:d; when two ratios are equal, then the cross products of the ratios are equal. that is, for the proportion, a:b = c:d , a x d = b x c. Proportion is an equality of two ratios. if four numbers are in proportion then the product of the extreme terms is equal to the product of the middle terms. three numbers a b c are said to be in continued proportion if a, b, b, c are in proportion. if a, b and c are in continued proportion then b is called the mean proportional between a and c. Cross multiplication is commonly first introduced as a way to check whether two fractions are equal, or equivalently whether an equation is a [true] proportion. for example, you might be given $$\frac{45}{67}=\frac{86}{128}$$ and asked whether it is a proportion (that is, whether it is true). Property 2 (means or extremes switching property): if a b = c d and is a proportion, then both d b = c a and a c = b d are proportions. example 3: 8 10 = 4 5 is a proportion. property 2 says that if you were to switch the 8 and 5 or switch the 4 and 10, then the new statement is still a proportion.
