Exponential Form To Logarithmic Form Shorts Algebra Math Maths Mathematics Lesson Howto

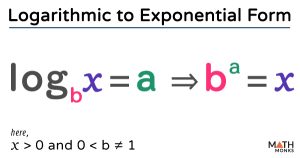
Logarithmic To Exponential Form Formulas And Examples Exponential form to logarithmic form #shorts #algebra #math #maths #mathematics #lesson #howto. Test your understanding of exponential & logarithmic functions with these 38 questions.

Ixl Convert Between Exponential And Logarithmic Form Grade 12 Maths If two logarithmic terms with the same base number (a above) are being added together, then the terms can be combined by multiplying the arguments (x and y above). Exponential to log form is useful to work across complicated exponential functions by transforming it into logarithmic functions. the multiplication or division of exponents is transformed into addition or subtraction with the help of logarithmic formulas. In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. To convert from exponential form to logarithmic form, identify the base of the exponential equation and move the base to the other side of the equal to sign, and add the word “log”.

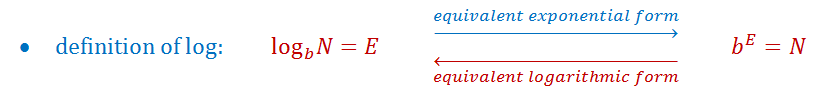
Convert From Exponential To Logarithmic Form Studypug In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. To convert from exponential form to logarithmic form, identify the base of the exponential equation and move the base to the other side of the equal to sign, and add the word “log”. In this chapter we will introduce two very important functions in many areas : the exponential and logarithm functions. we will look at their basic properties, applications and solving equations involving the two functions. In this section, we will learn techniques for solving exponential functions. the first technique involves two functions with like bases. recall that the one to one property of exponential functions tells us that, for any real numbers \ (b\), \ (s\), and \ (t\), where \ (b>0\), \ (b≠1\), \ (b^s=b^t\) if and only if \ (s=t\). No description has been added to this video. Converting from exponential form to natural logarithmic form is easier than you might think! follow along with this tutorial to see how to perform this conversion.

Master Converting Logarithmic To Exponential Form Studypug In this chapter we will introduce two very important functions in many areas : the exponential and logarithm functions. we will look at their basic properties, applications and solving equations involving the two functions. In this section, we will learn techniques for solving exponential functions. the first technique involves two functions with like bases. recall that the one to one property of exponential functions tells us that, for any real numbers \ (b\), \ (s\), and \ (t\), where \ (b>0\), \ (b≠1\), \ (b^s=b^t\) if and only if \ (s=t\). No description has been added to this video. Converting from exponential form to natural logarithmic form is easier than you might think! follow along with this tutorial to see how to perform this conversion.