Exponents And Indices Definitions Notation Laws Of Exponents Or

Class 6 Laws Of Exponents And Indices Exponentiation is defined as the mathematical operation of raising a quantity to the power of another quantity. exponential notation, base, and power are the three main primary concepts to learn the exponents. exponents are often identified as powers or indices. The exponent laws, also called the laws of indices (higgens 1998) or power rules (derbyshire 2004, p. 65), are the rules governing the combination of exponents (powers).
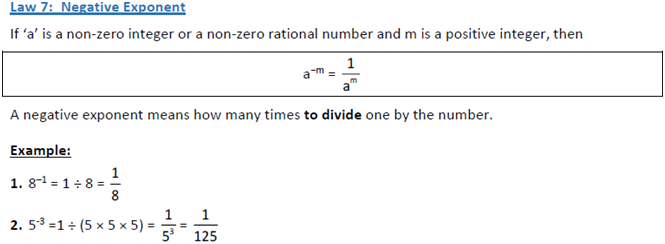
Class 6 Laws Of Exponents And Indices The definition of exponentiation can be extended in a natural way (preserving the multiplication rule) to define for any positive real base and any real number exponent . more involved definitions allow complex base and exponent, as well as certain types of matrices as base or exponent. Exponent rules are those laws that are used for simplifying expressions with exponents. learn about exponent rules, the zero rule of exponent, the negative rule of exponent, the product rule of exponent, and the quotient rule of exponent with the solved examples, and practice questions. Learning objectives review the rules of exponents. review the definition of negative exponents and zero as an exponent. work with numbers using scientific notation. By using exponents for repeated multiplication, you make expressions easier to read, write, and work with. indices (exponents) are calculated after brackets but before all basic operations. when an expression has brackets, evaluate the brackets first: $$ (2 \times 5)^2 $$ $$ (10)^2 $$ $$ 100 $$.

Class 6 Laws Of Exponents And Indices Learning objectives review the rules of exponents. review the definition of negative exponents and zero as an exponent. work with numbers using scientific notation. By using exponents for repeated multiplication, you make expressions easier to read, write, and work with. indices (exponents) are calculated after brackets but before all basic operations. when an expression has brackets, evaluate the brackets first: $$ (2 \times 5)^2 $$ $$ (10)^2 $$ $$ 100 $$. In mathematics indices or index is the value that is raised to the power of any variable or constant like x raised to power 2 i.e. x 2. where x is a variable and 2 is called the power or exponent of that variable. Exponents are a short hand notation used to represent many factors multiplied together. all of the rules for manipulating exponents may be deduced from the laws of multiplication and division that you are already familiar with. In the notation "a^b," the letter 'a' is called the base, and 'b' is called the exponent or index. the exponent tells us how many times the base should be multiplied by itself. Indices, also known as exponents or powers, represent the number of times a number (the base) is multiplied by itself. for example, in the expression 2^3, 2 is the base and 3 is the index, meaning 2 is multiplied by itself three times: 2 × 2 × 2 = 8.

Class 6 Laws Of Exponents And Indices In mathematics indices or index is the value that is raised to the power of any variable or constant like x raised to power 2 i.e. x 2. where x is a variable and 2 is called the power or exponent of that variable. Exponents are a short hand notation used to represent many factors multiplied together. all of the rules for manipulating exponents may be deduced from the laws of multiplication and division that you are already familiar with. In the notation "a^b," the letter 'a' is called the base, and 'b' is called the exponent or index. the exponent tells us how many times the base should be multiplied by itself. Indices, also known as exponents or powers, represent the number of times a number (the base) is multiplied by itself. for example, in the expression 2^3, 2 is the base and 3 is the index, meaning 2 is multiplied by itself three times: 2 × 2 × 2 = 8.

Class 6 Laws Of Exponents And Indices In the notation "a^b," the letter 'a' is called the base, and 'b' is called the exponent or index. the exponent tells us how many times the base should be multiplied by itself. Indices, also known as exponents or powers, represent the number of times a number (the base) is multiplied by itself. for example, in the expression 2^3, 2 is the base and 3 is the index, meaning 2 is multiplied by itself three times: 2 × 2 × 2 = 8.
Comments are closed.