Extremum D Une Fonction Exercice De Fonctions 717299 Décrire les variations de la fonction$g$. $\quad$ comparer lorsque cela est possible : • $g( 3)$ et $g( 1)$ • $g(1)$ et $g(3)$ $\quad$ lire le maximum de $g$ sur $[0;4]$ et le minimum de $g$ sur $[ 3;4]$. $\quad$ tracer une courbe susceptible de représenter graphiquement la fonction $g$. Le sens de variation (croissant ou décroissant) d’une fonction est résumé dans son tableau de variations. exemple : on connaît une fonction ƒ définie sur [0 ; ∞[ par sa représentation graphique ci dessous :.

Extremum Fonction Exercice De Mathématiques De Licence Maths 1e Ann 1. on vérifie que la fonction est dérivable et on calcule sa dérivée ; 2. on détermine les valeurs de x pour lesquelles la dérivée s'annule en changeant de signe ; 3. on en déduit les extremums en lisant les images des valeurs obtenues à l'étape précédente. Etudier les variations ou le sens de variation d ’une fonction, c ’est déterminer les intervalles sur lesquels elle est strictement croissante, strictement décroissante. ces résultats sont alors résumés dans un tableau de variation. Les variations de fonctions et les extremums à travers un cours de maths en 2de avec la croissance et décroissance d’une fonction ainsi que le tableau de variation. nous étudierons, dans cette leçon en seconde, l’aspect algébrique puis l’aspect graphique de l’étude des variations. Voici un exercice niveau seconde sur les variations et les extrémums d’une fonction. il faudra d’abord dresser le tableau de variations d’une fonction à partir de sa courbe. puis il faudra déterminer les extremums dès la fonction, c’est à dire son maximum et son minimum.

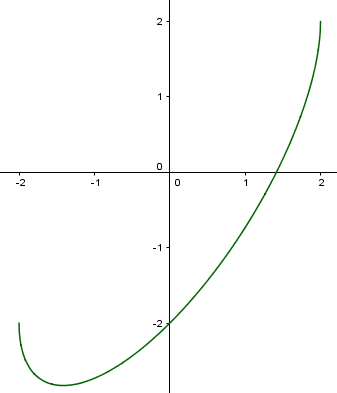
Notion D Extremum Local Les variations de fonctions et les extremums à travers un cours de maths en 2de avec la croissance et décroissance d’une fonction ainsi que le tableau de variation. nous étudierons, dans cette leçon en seconde, l’aspect algébrique puis l’aspect graphique de l’étude des variations. Voici un exercice niveau seconde sur les variations et les extrémums d’une fonction. il faudra d’abord dresser le tableau de variations d’une fonction à partir de sa courbe. puis il faudra déterminer les extremums dès la fonction, c’est à dire son maximum et son minimum. Maths au lycée en classe de seconde avec un cadre. l'élève a ici tous les outils pour comprendre les variations et les extrémums d'une fonction avec des vidéos courtes pour expliquer les bases et des corrections d'exercices complets avec logiciels dynamiques dès que possible. Il est possible de déterminer les extrema d'une fonction sur un intervalle. il s'agit soit du maximum d'une fonction sur un intervalle ou du minimum d'une fonction sur un intervalle. Dresser le tableau de variation d’une fonction à partir de sa courbe représentative. déterminer graphiquement les extrémums d’une fonction sur un intervalle. pour une fonction dont le tableau de variation est donné, comprendre un algorithme d’approximation numérique d’un extremum. Déterminer le maximum de la fonction f de l’exercice précédent sur [− 2; 2]. d’après la représentation graphique de la fonction f, son maximum est atteint en − 1 et vaut f (− 1) = 3. fonctions usuelles fonctions affines propriété. soit f: x ↦ a x b une fonction affine telle que a = 0. alors le tableau de variations de f.

Extremum Maths au lycée en classe de seconde avec un cadre. l'élève a ici tous les outils pour comprendre les variations et les extrémums d'une fonction avec des vidéos courtes pour expliquer les bases et des corrections d'exercices complets avec logiciels dynamiques dès que possible. Il est possible de déterminer les extrema d'une fonction sur un intervalle. il s'agit soit du maximum d'une fonction sur un intervalle ou du minimum d'une fonction sur un intervalle. Dresser le tableau de variation d’une fonction à partir de sa courbe représentative. déterminer graphiquement les extrémums d’une fonction sur un intervalle. pour une fonction dont le tableau de variation est donné, comprendre un algorithme d’approximation numérique d’un extremum. Déterminer le maximum de la fonction f de l’exercice précédent sur [− 2; 2]. d’après la représentation graphique de la fonction f, son maximum est atteint en − 1 et vaut f (− 1) = 3. fonctions usuelles fonctions affines propriété. soit f: x ↦ a x b une fonction affine telle que a = 0. alors le tableau de variations de f.
