
Solved Question 17 O F Is Injective And F Is Surjective O F Is Since, f(x) f (x) and f(x′) ∈ b f (x ′) ∈ b and f(x) = f(x′) f (x) = f (x ′), it follows that x =x′ x = x ′, by our assumption. thus, f f is injective. therefore, f f is invective if and only if for all y ∈ b y ∈ b there exists at most one x ∈ a x ∈ a such that f(x) = y f (x) = y is true. please critique this proof and give any advice. thank you!. In this video i do a fun proof involving injective functions and set theory.00:00 forward direction of proof4:48 backwards direction of proof.

Solved For 2b Prove That F Is Injective And Give A Specific Chegg Claim: f is injective if and only if it has a left inverse. proof: we must ( ⇒ ) prove that if f is injective then it has a left inverse, and also ( ⇐ ) that if f has a left inverse, then it is injective. The proof for f being surjective if and only if f(f 1) (y)) = y for all y⊆b is similar, but with the concepts of surjectivity and inverse images. explanation: in order to prove that f is injective if and only if x = (f 1) (f(x)) for all x⊆a, we need to prove both directions of the statement. A function f is injective if and only if whenever f(x) = f(y), x = y. example: f ( x ) = x 5 from the set of real numbers to is an injective function. is it true that whenever f(x) = f(y) , x = y ?. F is injective if and only if f has a left inverse. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.

Solved Prove That If Fтишg Is Injective Then G Is Injective Chegg A function f is injective if and only if whenever f(x) = f(y), x = y. example: f ( x ) = x 5 from the set of real numbers to is an injective function. is it true that whenever f(x) = f(y) , x = y ?. F is injective if and only if f has a left inverse. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. F(x) = f(y) implies x = y. we therefore let x;y 2 abe given such that f(x) = f(y). applying g to both sides and using the fact that g is a left inverse, we obtain x = g(f(x)) = g(f(y)) = y; as desired. since x and y were arbitrary, we have shown that f is injective. (2): we again let f : a ! b be given. suppose rst that f is surjective. then. The composition of two injective functions is injective, and the the composition of two surjective functions is surjective > and hence the same for two bijective functions. also recall that a function : → is bijective if and only if it has an inverse −1 : → . Now, a function f is said to be one to one, or injunction, if and only if f(a)=f(b) such that a=b for all a and b in the domain in f. all this means is that for a function to be one to one every distinct element in a has a distinct image in b. Prove that "injective function $f:x\to y$ exists" and "surjective function $g:y\to x$ exists" is logically equivalent. 0 for any function $v,$if $v \circ f$ is injective, then $f$ is injective.
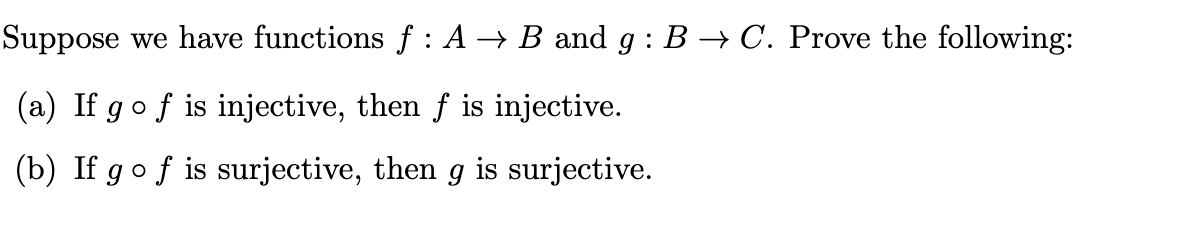
Solved Suppose We Have Functions F A B And G B C Chegg F(x) = f(y) implies x = y. we therefore let x;y 2 abe given such that f(x) = f(y). applying g to both sides and using the fact that g is a left inverse, we obtain x = g(f(x)) = g(f(y)) = y; as desired. since x and y were arbitrary, we have shown that f is injective. (2): we again let f : a ! b be given. suppose rst that f is surjective. then. The composition of two injective functions is injective, and the the composition of two surjective functions is surjective > and hence the same for two bijective functions. also recall that a function : → is bijective if and only if it has an inverse −1 : → . Now, a function f is said to be one to one, or injunction, if and only if f(a)=f(b) such that a=b for all a and b in the domain in f. all this means is that for a function to be one to one every distinct element in a has a distinct image in b. Prove that "injective function $f:x\to y$ exists" and "surjective function $g:y\to x$ exists" is logically equivalent. 0 for any function $v,$if $v \circ f$ is injective, then $f$ is injective.

Solved Useful Definitions Injective The Function F A B Chegg Now, a function f is said to be one to one, or injunction, if and only if f(a)=f(b) such that a=b for all a and b in the domain in f. all this means is that for a function to be one to one every distinct element in a has a distinct image in b. Prove that "injective function $f:x\to y$ exists" and "surjective function $g:y\to x$ exists" is logically equivalent. 0 for any function $v,$if $v \circ f$ is injective, then $f$ is injective.
