F3 Math 07 04 Orthogonal Projections Part 4 Jom Tuisyen

F3 Math 07 04 Orthogonal Projections Part 4 Jom Tuisyen Topic 07: plans and elevations f3 math 07 01 orthogonal projections f3 math 07 02 orthogonal projections (part 2) f3 math 07 03 orthogonal projections (part 3) f3 math 07 04 orthogonal projections (part 4). The document discusses orthogonal projections and plans and elevations. it covers what a plane and normal to a plane are, and examples of determining normals to different planes.

F3 Math 07 01 Orthogonal Projections Jom Tuisyen About press copyright contact us creators advertise developers terms privacy policy & safety how works test new features nfl sunday ticket © 2025 google llc. For an exercise, i need to investigate the orthogonal projection in more detail. i know that this has probably been discussed many times here, i am though interested in whether my explanations suffice and in particular in tasks 3 and 4. Find the orthogonal complement of a subspace. in this section, we compute orthogonal projections of vectors onto subspaces. an important use of the gram schmidt process is in orthogonal projections, the focus of this section. Theorem 2.58. a projection t ∈ l(v) is orthogonal if and only if it is self adjoint t = t∗. are orthogonal subspaces. letting x, y v and using subscripts to denote r(t) and n t(y) = xn, yr = xr, yr yn = t(x), y =⇒ t∗ = t a self adjoint projection. by the fun.

Solved Exercise 1 Orthogonal Projections 3 3 3 4 6 3 Chegg Find the orthogonal complement of a subspace. in this section, we compute orthogonal projections of vectors onto subspaces. an important use of the gram schmidt process is in orthogonal projections, the focus of this section. Theorem 2.58. a projection t ∈ l(v) is orthogonal if and only if it is self adjoint t = t∗. are orthogonal subspaces. letting x, y v and using subscripts to denote r(t) and n t(y) = xn, yr = xr, yr yn = t(x), y =⇒ t∗ = t a self adjoint projection. by the fun. This content is for members with subscription.log in register ← previous post next post →. F3 math 07 07 plans and elevations (part 2) this content is for members with subscription. A nonzero vector ~a is de ned to be orthogonal or perpendicular or normal to a nonzero vector ~b, if the angle from ~a to ~b is equal to the angle from ~b to ~a. why use the dot product? if the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as ~a. It defines orthogonal projections as the projection of a 3d object onto a plane such that the relative lengths and angles between lines are preserved. it contains exercises on determining plane types, matching orthogonal projections to planes, and drawing plans and elevations of 3d objects.

Proyeksi Ortogonal Pandangan Dan Konsep Dasar Pdf This content is for members with subscription.log in register ← previous post next post →. F3 math 07 07 plans and elevations (part 2) this content is for members with subscription. A nonzero vector ~a is de ned to be orthogonal or perpendicular or normal to a nonzero vector ~b, if the angle from ~a to ~b is equal to the angle from ~b to ~a. why use the dot product? if the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as ~a. It defines orthogonal projections as the projection of a 3d object onto a plane such that the relative lengths and angles between lines are preserved. it contains exercises on determining plane types, matching orthogonal projections to planes, and drawing plans and elevations of 3d objects.

Solved Find Matrices Of Orthogonal Projections Onto All 4 Chegg A nonzero vector ~a is de ned to be orthogonal or perpendicular or normal to a nonzero vector ~b, if the angle from ~a to ~b is equal to the angle from ~b to ~a. why use the dot product? if the angle between ~a and ~b is less than 90 degrees, then p~a(~b) points in the same direction as ~a. It defines orthogonal projections as the projection of a 3d object onto a plane such that the relative lengths and angles between lines are preserved. it contains exercises on determining plane types, matching orthogonal projections to planes, and drawing plans and elevations of 3d objects.
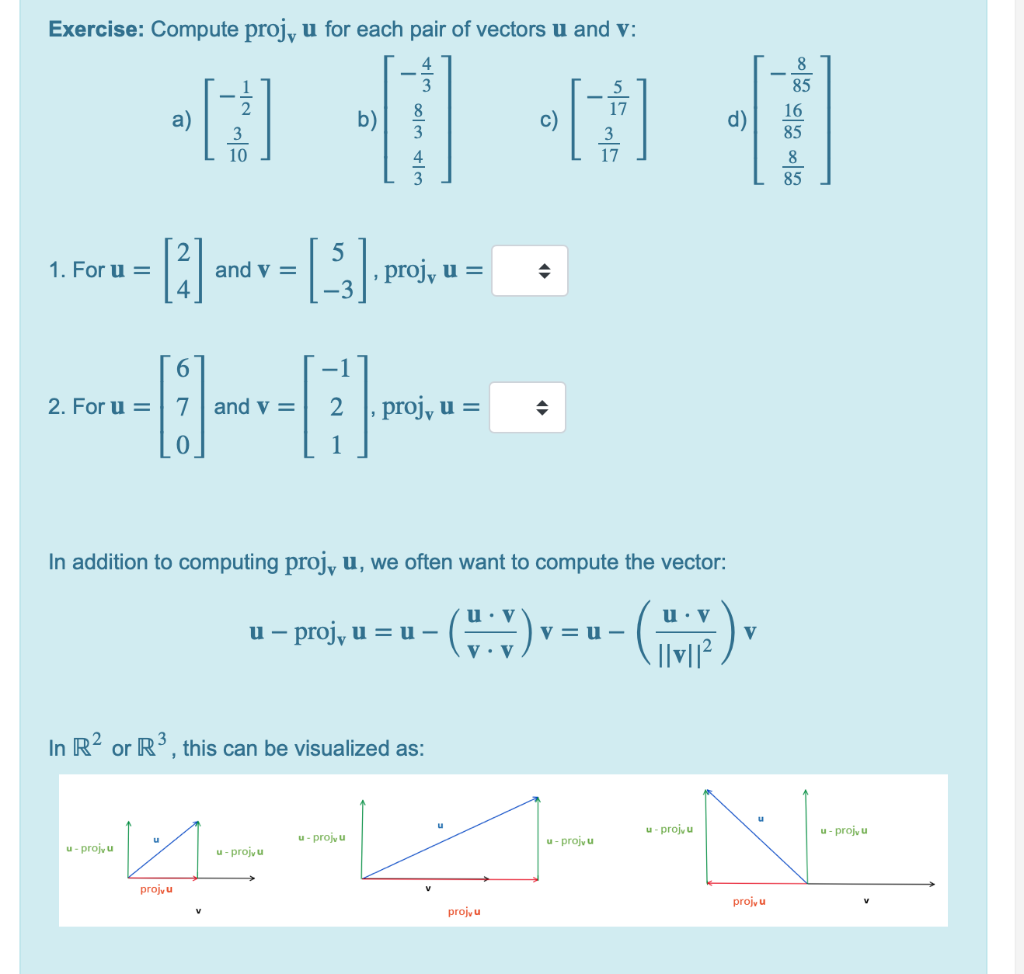
Solved Question 4 Orthogonal Projections Not Complete Marked Chegg
Comments are closed.