
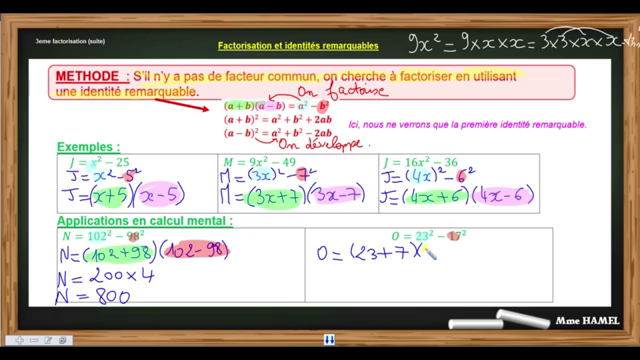
Méthode Simple Pour Factoriser Avec Une Identité Remarquable Comment factoriser une expression avec les identités remarquables? 1. qu'est ce que factoriser (rappel)? factoriser, c’est transformer une somme ou une différence en un produit. cela permet de simplifier des calculs ou de résoudre des équations. exemple : x 2 − 4 = (x − 2) (x 2) x^2 4 = (x 2)(x 2) 2. les identités remarquables. Factoriser à l’aide des identités remarquables mettre en pratique page 21 du chapitre 1, livre 3ème 3ème identité remarquable a2−b2 dans cet exercice, il faut voir que : le terme (x 5) correspond au terme « a ème» de la 3 identité remarquable ; le terme (x 5) 2 correspond donc au terme « a2 » de cette 3ème identité.
Podeduc Factoriser Identité Remarquable A B A B Niveau: lycéechapitre: calcul littéralcette vidéo vous présente comment factoriser à l’aide des identités remarquables.n'oubliez pas qu'avec j'ai 20 en m. 3eme exercices factoriser avec les identités remarquables corrigé exercice 1 : factoriser à l’aide de l’identité remarquable : pa`bq 2 “ a 2 `2ab`b 2 . Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$. 🔑 les étapes pour factoriser : identifier une identité remarquable : cherche si l’expression correspond à l’une des trois formules vues plus haut. mettre en facteur : si une identité remarquable ne s’applique pas directement, essaie de mettre en facteur le plus grand commun diviseur (pgcd). 💡 exemple 2 : factoriser une.

2nde Factoriser à L Aide D Une Identité Remarquable Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$. 🔑 les étapes pour factoriser : identifier une identité remarquable : cherche si l’expression correspond à l’une des trois formules vues plus haut. mettre en facteur : si une identité remarquable ne s’applique pas directement, essaie de mettre en facteur le plus grand commun diviseur (pgcd). 💡 exemple 2 : factoriser une. La première chose à faire pour factoriser des expressions avec les identités remarquables, c'est de connaître ces identités. on vous les a remises sur une fiche, il faut les apprendre par cœur. ensuite, quand vous avez une expression comme celle ci, vous devez déterminer comment la factoriser. Factoriser avec une identité remarquable. méthode pour factoriser une identité remarquable. soient a et b deux nombres quelconques, on a l’identité remarquable : a^2 b^2=(a b)(a b) pour factoriser à l’aide de cette identité remarquable : ① on repère l’identité remarquable comme la différence de deux carrés ; ② on identifie a. Factoriser en utilisant la 3ème identité remarquable pour tous nombres a et b : a² – b² = (a b)(a b) exemples 1 : il faut d'abord savoir repérer des carrés.
