
Méthode Simple Pour Factoriser Avec Une Identité Remarquable Lorsque cela est possible, factoriser les expressions suivantes en utilisant des identités remarquables. $\quad$ cette expression ressemble à $a^2 2ab b^2$ mais le signe $ $ ne porte pas sur le terme associé au double produit. on ne peut donc pas utiliser cette identité remarquable. Exercice 8: factoriser une expression à l'aide d'une identité remarquable $a^2 2ab b^2$ mathématiques seconde factoriser les expressions suivantes: $\color{red}{\textbf{a.
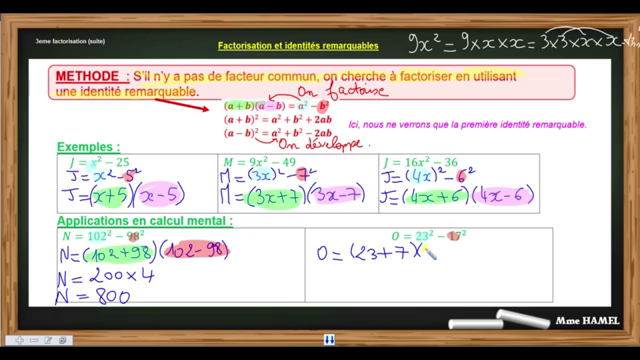
Podeduc Factoriser Identité Remarquable A B A B Factoriser une expression avec des identités remarquables. factoriser une expression numérique ou littérale, c’est l’écrire sous la forme d’un produit. avec k, a et b trois nombres quelconques. les identités remarquables rencontrées lors des développements vont aussi nous permettre de factoriser des expressions. Factoriser une expression consiste à tranformer les sommes et différences en produits. dans les expressions précédentes des identités remarquables, le terme de gauche de l'égalité est factorisé, celui de droite est développé. exercices. factoriser les expressions suivantes:. Factoriser en utilisant l’identité remarquable : a2 −b2 = (a−b)(a b). a = 4x2 −9. b = 16−9x2. c = 49x2 −36. d = (x 1)2 −4. e = (2x 1)2 −25. f = 36−(4−3x)2. exercice n 7 factoriser d’abord l’expression soulignée pour retrou ver le facteur commun : a = (x 2)(3x−1) x2 −4. b = (x 4)(2x−1) x2 −16. c = (2x 1)(x−2. Distributivité : (a b)(c d)=(a b)×c (a b)×d=ac bc ad db=ac ad bc bd (c) utiliser éventuellement le tableau de multiplication pour développer, réduire et ordonner les expressions suivantes au maximum.

Podeduc Coopmaths Correction Exercices 2n41 7 Factoriser Avec Une Factoriser en utilisant l’identité remarquable : a2 −b2 = (a−b)(a b). a = 4x2 −9. b = 16−9x2. c = 49x2 −36. d = (x 1)2 −4. e = (2x 1)2 −25. f = 36−(4−3x)2. exercice n 7 factoriser d’abord l’expression soulignée pour retrou ver le facteur commun : a = (x 2)(3x−1) x2 −4. b = (x 4)(2x−1) x2 −16. c = (2x 1)(x−2. Distributivité : (a b)(c d)=(a b)×c (a b)×d=ac bc ad db=ac ad bc bd (c) utiliser éventuellement le tableau de multiplication pour développer, réduire et ordonner les expressions suivantes au maximum. Elles sont comme des « raccourcis » pour effectuer des calculs plus rapidement. voici les trois identités remarquables que tu dois connaître en classe de seconde : le carré d’une somme : (a b)² = a² 2ab b²; le carré d’une différence : (a b)² = a² 2ab b²; le produit d’une somme et d’une différence : (a b)(a. Cours de maths sur les identités remarquables. au programme, identités remarquables et exemples d'application pour les développements et factorisations. La première chose à faire pour factoriser des expressions avec les identités remarquables, c'est de connaître ces identités. on vous les a remises sur une fiche, il faut les apprendre par cœur. ensuite, quand vous avez une expression comme celle ci, vous devez déterminer comment la factoriser. Divers exercices autour des identités remarquables : développement, factorisation équation, forme canonique, exercices de recherche.

2nde Factoriser à L Aide D Une Identité Remarquable Elles sont comme des « raccourcis » pour effectuer des calculs plus rapidement. voici les trois identités remarquables que tu dois connaître en classe de seconde : le carré d’une somme : (a b)² = a² 2ab b²; le carré d’une différence : (a b)² = a² 2ab b²; le produit d’une somme et d’une différence : (a b)(a. Cours de maths sur les identités remarquables. au programme, identités remarquables et exemples d'application pour les développements et factorisations. La première chose à faire pour factoriser des expressions avec les identités remarquables, c'est de connaître ces identités. on vous les a remises sur une fiche, il faut les apprendre par cœur. ensuite, quand vous avez une expression comme celle ci, vous devez déterminer comment la factoriser. Divers exercices autour des identités remarquables : développement, factorisation équation, forme canonique, exercices de recherche.
