Les Identités Remarquables Leçon Apprentivore Identités remarquables, application directe des formules. exercice 1 : factorisez les expressions suivantes. exercice 2 : développez les expressions suivantes. En effet, ici on peut développer (2x 1) 2 avec la première formule (a=2x, b=1) et (3x 7) 2 avec la première formule (a=3x et b=7), mais on peut aussi factoriser en utilisant la troisième formule avec a = 2x 1 et b = 3x 7 ! voyons les deux méthodes : tout d’abord si l’on demande de développer :.

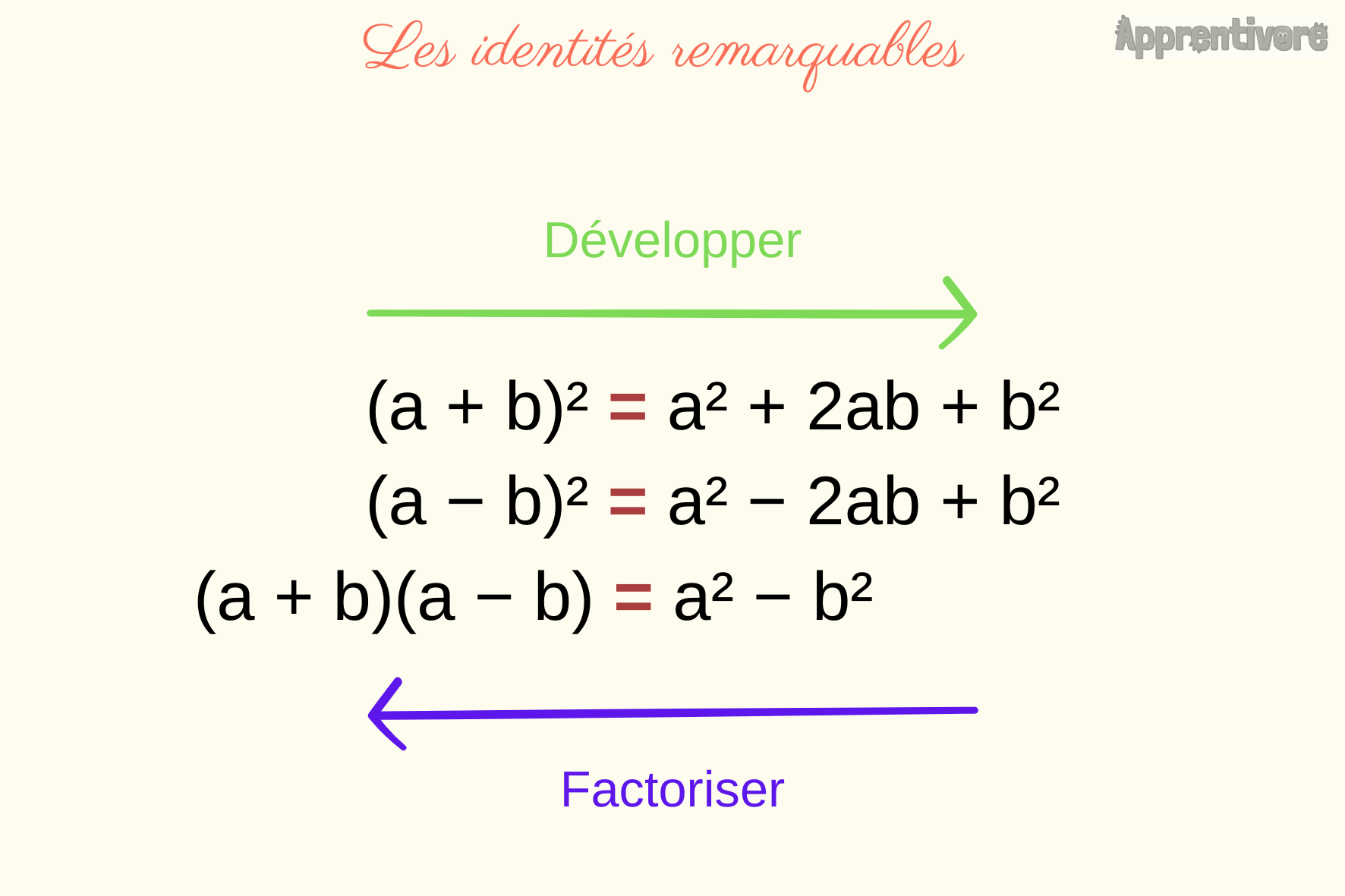
Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Pour factoriser une expression en utilisant les identités remarquables, il convient d’écrire directement l’expression finale sans l’étape intermédiaire qui doit être effectuée mentalement. Les identités remarquables (3e) elles sont très utiles pour développer ou factoriser des expressions littérales rapidement. il faut les connaître dans les 2 sens. 1) carré d'une somme (a b)² = a² 2 × a × b b²; noté aussi : (a b)² = a² 2ab b². a² b² : somme des carrés. 2 × a × b ou 2ab : double produit. exemples. Cours gratuit sur les identités remarquables, le développement et la factorisation, maths niveau troisième. Ii. factorisations en appliquant les identités remarquables 1) les identités remarquables on applique une identité remarquable pour factoriser. rappel : a2 2ab b2 = (a b)2 a2 – 2ab b2 = (a – b)2 a2 – b2 = (a – b)(a b).

Les Identités Remarquables Cours Dyrassa Factoriser Et Développer Cours gratuit sur les identités remarquables, le développement et la factorisation, maths niveau troisième. Ii. factorisations en appliquant les identités remarquables 1) les identités remarquables on applique une identité remarquable pour factoriser. rappel : a2 2ab b2 = (a b)2 a2 – 2ab b2 = (a – b)2 a2 – b2 = (a – b)(a b). Identités remarquables factoriser. rappel des trois identités remarquables: 1) a² 2ab b² = (a b)². exemple: 9x² 6x 1 = (3x 1)². Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$. Factoriser avec les identités remarquables (programme de seconde) la deuxième manière consiste à utiliser les identités remarquables. pour rappel, les identités remarquables sont : $(a b)^2 = a^2 2ab b^2$ $(a b)^2 = a^2 – 2ab b^2$ $(a b)(a – b) = a^2 – b^2$ exemple : factoriser l’expression $4x^2 12x 9$.

Solution Cours Developpement Factorisation Et Identites Remarquables 3 Identités remarquables factoriser. rappel des trois identités remarquables: 1) a² 2ab b² = (a b)². exemple: 9x² 6x 1 = (3x 1)². Pour factoriser avec une identité remarquable, on utilise une des trois formules vues précédemment dans le sens inverse par rapport au développement : $ a^2 2ab b^2=(a b)^2$ $ a^2 2ab b^2=(a b)^2$. Factoriser avec les identités remarquables (programme de seconde) la deuxième manière consiste à utiliser les identités remarquables. pour rappel, les identités remarquables sont : $(a b)^2 = a^2 2ab b^2$ $(a b)^2 = a^2 – 2ab b^2$ $(a b)(a – b) = a^2 – b^2$ exemple : factoriser l’expression $4x^2 12x 9$.
