
Lambert W Function From Wolfram Mathworld On the interval −1 e < x < 0, w(x) has two distinct real values, de picted as w0(x) and w−1(x), which can be determined (approximately) with a computer program, such as wolframalpha (using productlog[ ]). w0(e) = w(1 · e1) = 1. w0(−e−1) = −1. w0(e1 e) = e. w0(e1 2 ) = 1 2. n 1 n. w0(1) ≡ Ω = e−w0(1) = − ln w0(1) ≈ 0.567143. If you can solve one equation involving exponential functions you can bootstrap your solution solve a lot more equations. the lambert w function is defined to be the function w(x) that maps each x to a solution of the equation. w exp(w) = x. this function is implemented python under scipy.special.lambertw. let’s see how we could use it solve.

Lambert W Function From Wolfram Mathworld The lambert w function has infinitely many branches. for $ 1 e < x < 0$, both the "$ 1$" branch $w { 1}$ and the "$0$" branch $w 0$ are real; both are $ 1$ at $ 1 e$, but $w { 1}(x)$ decreases to $ \infty$ as $x$ increases to $0$ while $w 0(x)$ increases to $0$. Using the function, we can solve both of our problems: a) )solve =𝐥𝐧( the general strategy is to get the equation in the form = 𝑏, before saying that 𝑊( )= by definition of the lambert w function. getting your expression in this form requires a certain degree of ingenuity. I'm attempting to solve the following equation (eventually with lambert's w function having checked the solution on wolfram alpha): 100n2 = 2n. i got as far as follows but i am unsure how to progress: ln100 2ln(n) = nln2. any suggestions would be much appreciated. We present a new discussion of the complex branches of w , an asymptotic expansion valid for all branches, an efficient numerical procedure for evaluating the function to arbitrary precision, and a method for the symbolic integration of expressions containing w . 1. introduction.
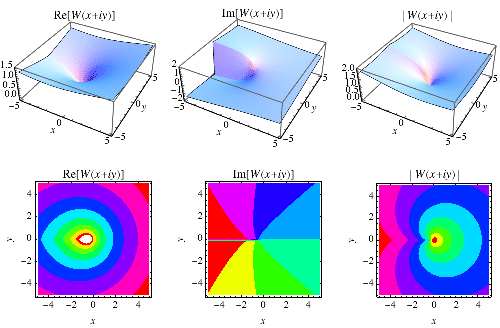
Lambert W Function From Wolfram Mathworld I'm attempting to solve the following equation (eventually with lambert's w function having checked the solution on wolfram alpha): 100n2 = 2n. i got as far as follows but i am unsure how to progress: ln100 2ln(n) = nln2. any suggestions would be much appreciated. We present a new discussion of the complex branches of w , an asymptotic expansion valid for all branches, an efficient numerical procedure for evaluating the function to arbitrary precision, and a method for the symbolic integration of expressions containing w . 1. introduction. Figure 1 real branches of the lambert wfunction. the solid line is the principal branch w0; the dashed line is −1, which is the only other branch that takes real values. the small filled circle at the branch point corresponds to the one in figure 2. the wright ωfunction helps to solve the equation y lny=z. we have that if z=t±iπfor t<−. The lambert w function is used to solve equations in which the unknown quantity occurs both in the base and in the exponent, or both inside and outside of a logarithm. We can learn quite a bit about the w function by plotting f, which can be done by specifying wand then computing xfrom (1). the matlab commands for this might be: w = [ 400:200]*0.01; x = w.*exp(w); plot(x,w,’b ’) axis([ 1 6 4 2]) grid on the last command lays a grid of dotted lines over the plot. the results are given in fig. 1 (next page). In pure mathematics, the w function is valuable in solving transcendental and differential equations, in combinatorics (as the tree function), for delay differential equations and for iterated epxonentials (which is the context in which we have introduced it).

Lambert W Function From Wolfram Mathworld Figure 1 real branches of the lambert wfunction. the solid line is the principal branch w0; the dashed line is −1, which is the only other branch that takes real values. the small filled circle at the branch point corresponds to the one in figure 2. the wright ωfunction helps to solve the equation y lny=z. we have that if z=t±iπfor t<−. The lambert w function is used to solve equations in which the unknown quantity occurs both in the base and in the exponent, or both inside and outside of a logarithm. We can learn quite a bit about the w function by plotting f, which can be done by specifying wand then computing xfrom (1). the matlab commands for this might be: w = [ 400:200]*0.01; x = w.*exp(w); plot(x,w,’b ’) axis([ 1 6 4 2]) grid on the last command lays a grid of dotted lines over the plot. the results are given in fig. 1 (next page). In pure mathematics, the w function is valuable in solving transcendental and differential equations, in combinatorics (as the tree function), for delay differential equations and for iterated epxonentials (which is the context in which we have introduced it).

Figure 1 From Simplified Lambert W Function Math Equations When Applied We can learn quite a bit about the w function by plotting f, which can be done by specifying wand then computing xfrom (1). the matlab commands for this might be: w = [ 400:200]*0.01; x = w.*exp(w); plot(x,w,’b ’) axis([ 1 6 4 2]) grid on the last command lays a grid of dotted lines over the plot. the results are given in fig. 1 (next page). In pure mathematics, the w function is valuable in solving transcendental and differential equations, in combinatorics (as the tree function), for delay differential equations and for iterated epxonentials (which is the context in which we have introduced it).
