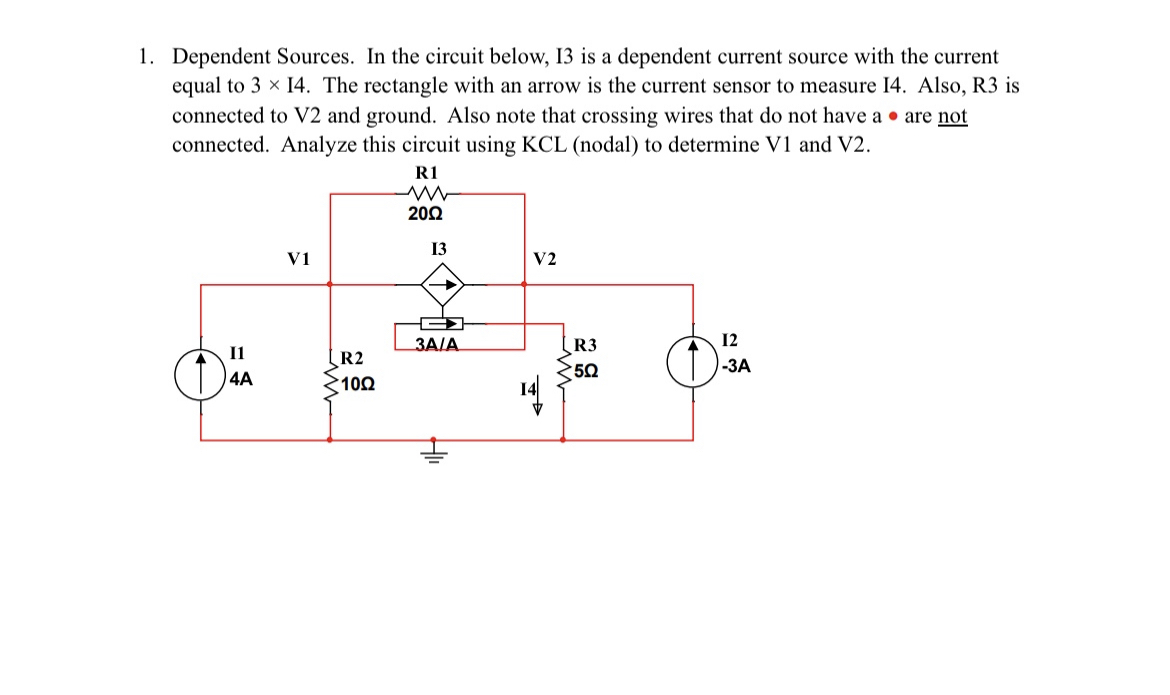
Dependent Sources In The Circuit Below I3 ï Is A Chegg Questiona. find the loop current i1 and i2b. find the value of the dependent sourcevisit smartbukites for more tutorial videos. This page provides a step by step introduction to using the mesh current method (also known as the loop current method) for analyzing electrical circuits. the mesh current method uses simultaneous equations, kirchhoff’s voltage law (kvl) , and ohm’s law to determine unknown currents in a network.
Solved Find Loop Currents I1 I2 I3 Is The Value Of Dependent Chegg In this lecture we will develop two very powerful methods for analyzing any circuit: the node method and the mesh method. these methods are based on the systematic application of kirchhoff’s laws. we will explain the steps required to obtain the solution by considering the circuit example shown on figure 1. figure 1. a typical resistive circuit. Let the current flowing through the two loops be [latex]i {1} [ latex] and [latex]i {2}[ latex], as shown in figure 5.22. by applying kvl [latex]sum{e}. Solve the resulting loop equations for the mesh currents. determine any requested current or voltage in the circuit using the mesh currents. let us illustrate the method by the following example: find the current i in the circuit below. we see that there are two meshes (or a left and right window) in this circuit. By solving equation 1 and equation 2, the value of i1 and i2 can be identified. now we will see two practical examples to solve the circuit loops. solving two meshes using mesh current analysis. what will be the mesh current of the following circuit? the above circuit network is slightly different than the previous example.

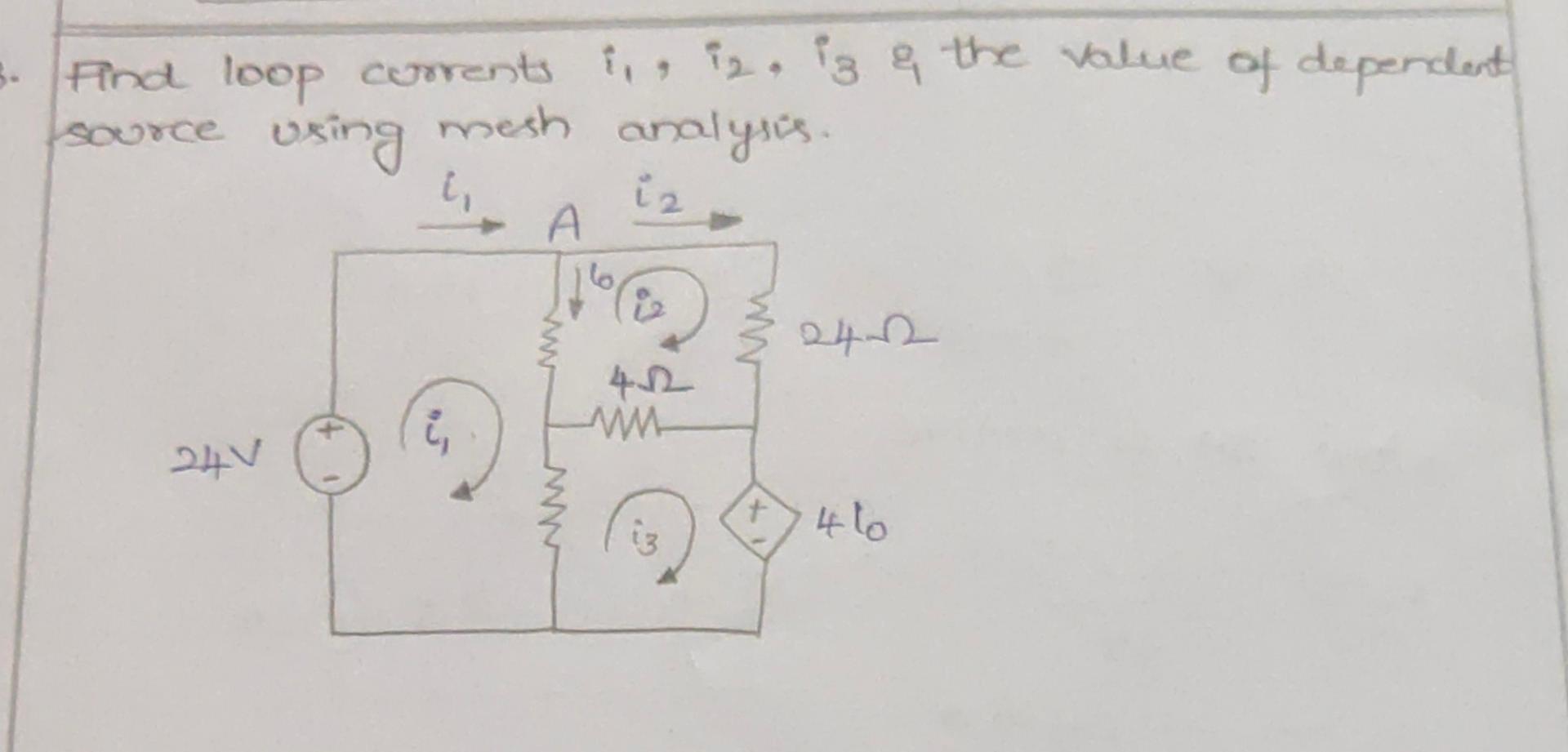
Solved Find The Current I2 Using The Node Voltages Method The Solve the resulting loop equations for the mesh currents. determine any requested current or voltage in the circuit using the mesh currents. let us illustrate the method by the following example: find the current i in the circuit below. we see that there are two meshes (or a left and right window) in this circuit. By solving equation 1 and equation 2, the value of i1 and i2 can be identified. now we will see two practical examples to solve the circuit loops. solving two meshes using mesh current analysis. what will be the mesh current of the following circuit? the above circuit network is slightly different than the previous example. We have on dependent source, which is at ##r 3##, so i'll label the current there ##i x## $$mesh 1: v s i 1r 1 i 1r 2 r 3(i 1 i 2)=0$$ $$mesh 2: v s i 2r 4 r 3(i 2 i 1) i 2r 5=0$$. For the loop containing v1, the dependent current source, and the resistor: v1 = i1 * 1Ω 2v2. express the currents in terms of the voltages using the y parameters. from the kcl equation: i1 = y11 * v1 y12 * v2. from the kvl equation: i2 = y21 * v1 y22 * v2. solve the equations to find the y parameters. y11 = 1Ω, y12 = 2, y21 = 0, y22 = 2. Here’s the best way to solve it. apply kirchhoff's voltage law (kvl) to mesh 1 to write the equation involving i 1, i 2, and i 3 by summing the voltage drops around the loop and setting them equal to zero. 3. find loop currents i1, i2, i3 and the value of dependent source using mesh analysis. ah % 24 92 24 v 41 10 92 4 1292 ww ¹ ₂ c. We must convert any current sources to equivalent voltage sources before we use the mesh format. instead of choosing convenient tracing loops, we draw a current loop for each mesh. all mesh currents must have the same direction, either clockwise or counterclockwise. the more common choice is clockwise.
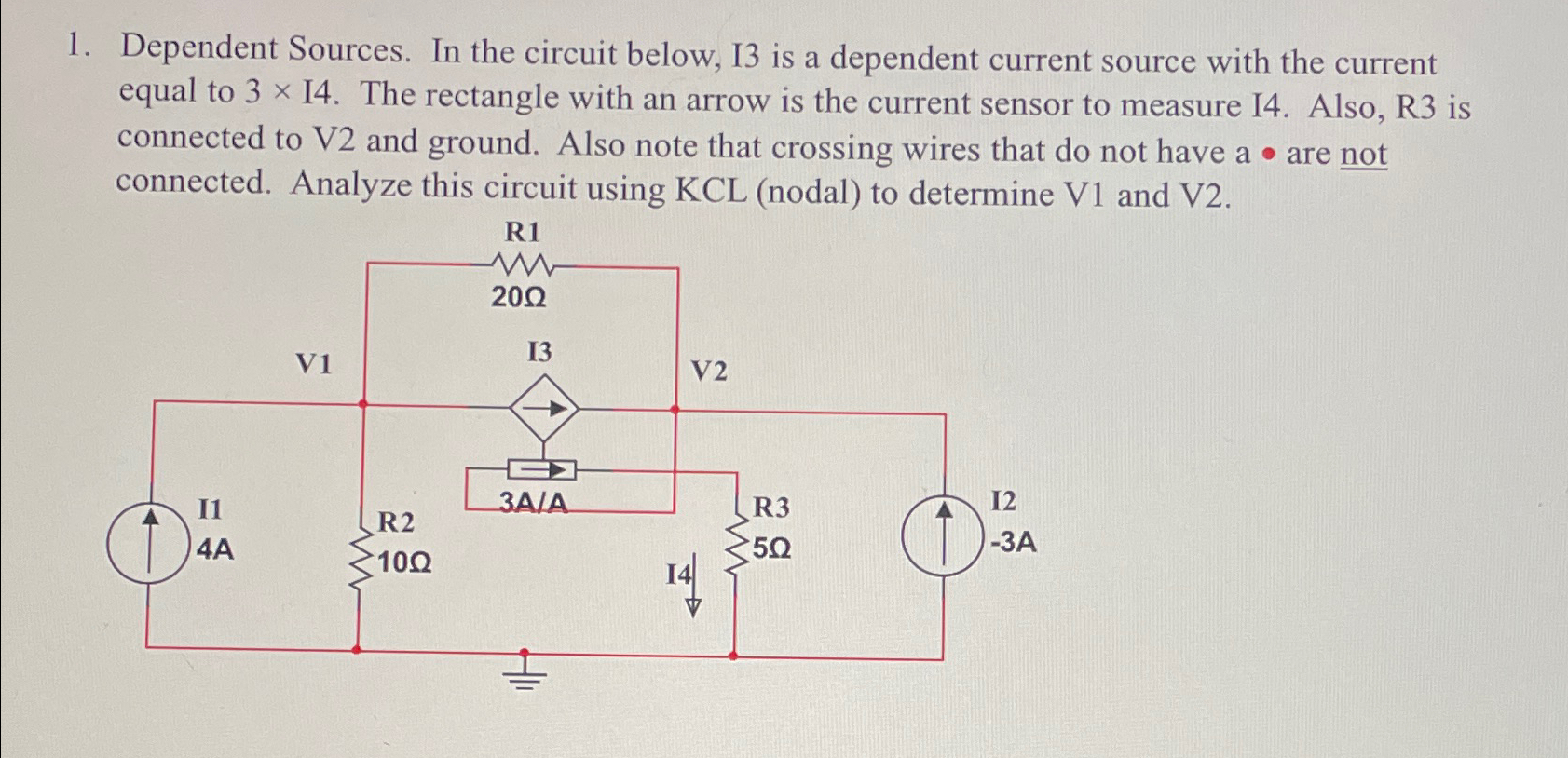
Solved Dependent Sources In The Circuit Below I3 ï Is A Chegg We have on dependent source, which is at ##r 3##, so i'll label the current there ##i x## $$mesh 1: v s i 1r 1 i 1r 2 r 3(i 1 i 2)=0$$ $$mesh 2: v s i 2r 4 r 3(i 2 i 1) i 2r 5=0$$. For the loop containing v1, the dependent current source, and the resistor: v1 = i1 * 1Ω 2v2. express the currents in terms of the voltages using the y parameters. from the kcl equation: i1 = y11 * v1 y12 * v2. from the kvl equation: i2 = y21 * v1 y22 * v2. solve the equations to find the y parameters. y11 = 1Ω, y12 = 2, y21 = 0, y22 = 2. Here’s the best way to solve it. apply kirchhoff's voltage law (kvl) to mesh 1 to write the equation involving i 1, i 2, and i 3 by summing the voltage drops around the loop and setting them equal to zero. 3. find loop currents i1, i2, i3 and the value of dependent source using mesh analysis. ah % 24 92 24 v 41 10 92 4 1292 ww ¹ ₂ c. We must convert any current sources to equivalent voltage sources before we use the mesh format. instead of choosing convenient tracing loops, we draw a current loop for each mesh. all mesh currents must have the same direction, either clockwise or counterclockwise. the more common choice is clockwise.
