
Find The Products Of The Following Using The Identity A B 2 Use the identity (x a) (x b) = x2 (a b)x ab to find the following products. (i) (x 3) (x 7) (ii) (4x 5) (4x 1) (iii) (4x 5) (4x 1) (iv) (4x 5) (4x 1) (v) (2x 5y) (2x 3 y) solution: we will be using the algebraic identity (x a) (x b) = x 2 (a b)x ab to solve the given questions. (i) (x 3) (x 7). See the identities to find the products of two binomials using the formulas. 1. use the formula (x a) (x b) = x 2 x(a b) ab to identity to find the following products.

Find The Products Of The Following Using The Identity A B 2 Let's go through each of the expressions and find their products using standard algebraic identities. i'll explain each one step by step. this expression follows the identity (a−b)2=a2−2ab b2. therefore, (a−b)2=a2−2ab b2. use the identity (a b)2=a2 2ab b2. here, a=2a and b=3b. (2a 3b)2=(2a)2 2(2a)(3b) (3b)2=4a2 12ab 9b2. Ex 2.4, 1 use suitable identities to find the following products: (iv) (y2 3 2 ) (y2 – 3 2 ) (y2 3 2 ) (y2 – 3 2) by using the identity (a b) (a – b) = a2 – b2 , where a = y2 , b = 3 2 = (y2)2 – (3 2)^2 = y4 – 9 4. We will use the given algebraic identities to find the products and evaluate the expressions step by step. using the identity (a b)2 =a2 2ab b2, we find the product for (3x 9)^2: (3x 9)2 =(3x)2 2(3x)(9) (9)2 = 9x2 54x 81. using the identity (a b)2 =a2 2ab b2, we find the product for (2x1 x)2: (2x1 x)2 =(2x1)2 2(2x1)(x) x2 = 4x21 1 x2. Using identity a2 2ab b2 (3x 9)2= 3x^2 2(3x)(9) 9^2 = 9x^2 54x 81. using the identity again 9x^2 54x 81 = 3x^2 9^2 2(3x)(9) = (3x 9) (3x 9).
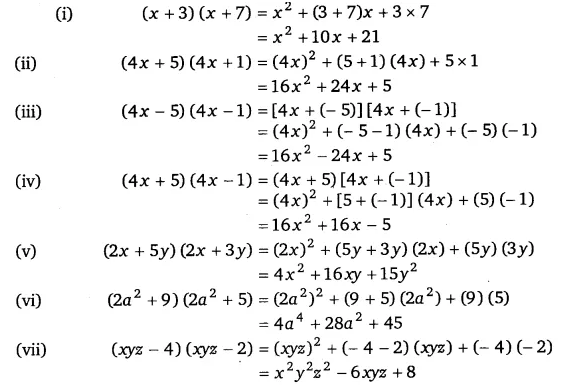
Use The Identity X A X B X2 A B X Ab To Find The We will use the given algebraic identities to find the products and evaluate the expressions step by step. using the identity (a b)2 =a2 2ab b2, we find the product for (3x 9)^2: (3x 9)2 =(3x)2 2(3x)(9) (9)2 = 9x2 54x 81. using the identity (a b)2 =a2 2ab b2, we find the product for (2x1 x)2: (2x1 x)2 =(2x1)2 2(2x1)(x) x2 = 4x21 1 x2. Using identity a2 2ab b2 (3x 9)2= 3x^2 2(3x)(9) 9^2 = 9x^2 54x 81. using the identity again 9x^2 54x 81 = 3x^2 9^2 2(3x)(9) = (3x 9) (3x 9). Find the product of the following using identity (a b)(a b)=a^2 b^2. a).(x p)(x p) 31248342. Using the identity (a b) (a – b) = a 2 – b 2, find the following product. (p 2) (p – 2) expansion of (a b) (a b) = a2 b2. is there an error in this question or solution? q 6. (i) q 5. (iv) q 6. (ii) exercise 3.1 | q 6. (i) | page 62. Use the identity (x a)(x b)=x2 (a b)x ab to find the following products : (i) (x 3)(x 7) (ii) (4x 5)(4x 1) abc d is a trapezium with ab ∥dc. a line parallel to ac intersects ab at x and bc at y. prove that ar( adx) =ar( ac y) a godown measures 40 m ×25 m ×15 m. Convert the following fraction into decimal by converting the fraction into an equivalent fraction with a denominator 10 100 or 1000 4 5.

Find The Products Using The Identity A B A B A 2 B 2 Find the product of the following using identity (a b)(a b)=a^2 b^2. a).(x p)(x p) 31248342. Using the identity (a b) (a – b) = a 2 – b 2, find the following product. (p 2) (p – 2) expansion of (a b) (a b) = a2 b2. is there an error in this question or solution? q 6. (i) q 5. (iv) q 6. (ii) exercise 3.1 | q 6. (i) | page 62. Use the identity (x a)(x b)=x2 (a b)x ab to find the following products : (i) (x 3)(x 7) (ii) (4x 5)(4x 1) abc d is a trapezium with ab ∥dc. a line parallel to ac intersects ab at x and bc at y. prove that ar( adx) =ar( ac y) a godown measures 40 m ×25 m ×15 m. Convert the following fraction into decimal by converting the fraction into an equivalent fraction with a denominator 10 100 or 1000 4 5.
