Find Two Consecutive Natural Numbers Whose Squares Have The Sum 221 Ex 4.2, 4 find two consecutive positive integers, sum of whose squares is 365. there is difference of 1 in consecutive positive integers let first integer = x ∴ second integer = x 1 given that sum of squares = 365 (first number)2 (second number)2 = 365 x2 (x 1)2. Step 1: let the first number be x. since the numbers are consecutive, hence next number will be: x 1. step 2: according to the given condition, sum of the squares of these two consecutive numbers is 365: ∴ (x) 2 (x 1) 2 = 365. ∴ x 2 x 2 2 x 1 = 365. ∴ 2 x 2 2 x 1 = 365. ∴ 2 x 2 2 x – 364 = 0. dividing by 2, we get:.

4 Find Two Consecutive Natural Numbers The Of Whose Squares Is 145 Find two consecutive positive integers, sum of whose squares is 365 [solved]. solution: let the first integer be x. the next consecutive positive integer will be x 1. according to the given question, the sum of squares of x and x 1 is 365. i.e., x 2 ( x 1) 2 = 365. x 2 (x 2 2x 1) = 365 [ ∵ (a b) 2 = a 2 2ab b 2]. 1 to find two consecutive natural numbers whose squares sum to 365, we start by defining the two numbers. let the first number be x x and the second number, being consecutive, will be x 1 x 1. Find the two consecutive positive integers, whose sum of squares is 365 ans: hint: we solve this problem by considering the required numbers as \\ ['n'\\] and \\ ['n 1'\\] because the required numbers should be consecutive. then we use the given cond. Break the coefficient of ‘x’ in such a way that their sum is equal to coefficient of ‘x’ and their product is equal to the product of coefficient of x 2 and the constant term. we can write 182 = 14 × 13. ∴ the two positive integers having sum of their squares 365 are 13 and 14.

Find Two Consecutive Natural Numbers Sum Of Whose Squares Is 365 Find the two consecutive positive integers, whose sum of squares is 365 ans: hint: we solve this problem by considering the required numbers as \\ ['n'\\] and \\ ['n 1'\\] because the required numbers should be consecutive. then we use the given cond. Break the coefficient of ‘x’ in such a way that their sum is equal to coefficient of ‘x’ and their product is equal to the product of coefficient of x 2 and the constant term. we can write 182 = 14 × 13. ∴ the two positive integers having sum of their squares 365 are 13 and 14. In that numbers, let one of the numbers be ’x’. it’s consecutive positive integer is (x 1) sum of their squares is 365. ∴ (x)2 (x 1)2 = 365 x2 x2 2x 1 = 365 2x2 2x 1 = 365 2x2 2x 1 – 365 = 0 2x2 2x – 365 = 0 x2 x – 182 = 0 x2 14x – 13x – 182 = 0 x (x 14) – 13 (x 14) = 0 (x 14) (x – 13) = 0. Let the two consecutive numbers be x and (x 1) sum of squares of these numbers is 365 ⇒x2 (x 1)2 = 365 ⇒x2 x2 2x 1 = 365 ⇒2x2 2x 1 – 365 = 0. Let the first number = x then the second number = x 1 according to the question , (x)² (x 1)²= 365 x² x² 1 2x = 365 2x² 2x 1 = 365 2x² 2x = 364 2x² 2x 364 = 0 2…. Product of two consecutive positive integers = 306 let first positive integer = x second positive integer = x 1 sum of squares of both consecutive numbers = 365 (x) 2 (x 1) 2 = 365 x 2 x 2 2x 1 = 365 2x 2 2x 1 = 365 2x 2 2x 1 365 = 0 2x 2 2x 364 = 0 2 (x 2 x 182) = 0 x 2 x 182 = 0 x 2 14x 13x 182 = 0.
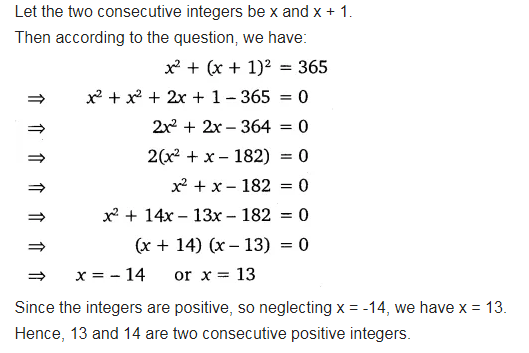
Find Two Consecutive Positive Integers Sum Of Whose Squares Is 365 In that numbers, let one of the numbers be ’x’. it’s consecutive positive integer is (x 1) sum of their squares is 365. ∴ (x)2 (x 1)2 = 365 x2 x2 2x 1 = 365 2x2 2x 1 = 365 2x2 2x 1 – 365 = 0 2x2 2x – 365 = 0 x2 x – 182 = 0 x2 14x – 13x – 182 = 0 x (x 14) – 13 (x 14) = 0 (x 14) (x – 13) = 0. Let the two consecutive numbers be x and (x 1) sum of squares of these numbers is 365 ⇒x2 (x 1)2 = 365 ⇒x2 x2 2x 1 = 365 ⇒2x2 2x 1 – 365 = 0. Let the first number = x then the second number = x 1 according to the question , (x)² (x 1)²= 365 x² x² 1 2x = 365 2x² 2x 1 = 365 2x² 2x = 364 2x² 2x 364 = 0 2…. Product of two consecutive positive integers = 306 let first positive integer = x second positive integer = x 1 sum of squares of both consecutive numbers = 365 (x) 2 (x 1) 2 = 365 x 2 x 2 2x 1 = 365 2x 2 2x 1 = 365 2x 2 2x 1 365 = 0 2x 2 2x 364 = 0 2 (x 2 x 182) = 0 x 2 x 182 = 0 x 2 14x 13x 182 = 0.
