
37 Formules Probabilités De Base Flashcards Quizlet Présentation et démonstration de la formule des probabilités composées théorème : soient $a 1,\dots,a m$ des événements tels que $p(a 1\cap\dots\cap a m)\neq 0$. alors : $$p(a 1\cap\dots\cap a m)=p(a 1)p(a 2|a 1)p(a 3|a 1\cap a 2)\cdots p(a m|a 1\cap \dots\cap a {m 1}).$$. En mathématiques, la formule des probabilités composées (ou formule des probabilités conditionnelles en cascade) permet de calculer la probabilité d’une intersection d’évènements (non nécessairement indépendants) à l’aide de probabilités conditionnelles.

Formule Des Probabilités Composées Principales formules de la probabilité conditionnelle 1. formule des probabilités composées découle directement de la définition de la probabilité conditionnelle. 20. Énoncer et démontrer la formule des probabilités composées. une urne contient initialement 7 boules noires et 3 boules blanches. on tire successivement 3 boules : si on tire une noire, on l'enlève, si on tire une blanche, on la retire, et on ajoute une noire à la place. Preuve : formule des probabilités composées soit $\mathcal h(n)$ la proposition : « pour toute famille $(b {1},\dots,b {n})$ d'événements tels que $\mathbb p(b {1}\cap\dots\cap b {n 1})\neq0$, on a $\mathbb p(b {1}\cap\dots\cap b {n})=\mathbb p(b {1})\times\mathbb p {b {1}}(b {2})\times\dots\times\mathbb p {b {1}\cap\dots\cap b {n 1}}(b {n. 2.4. formule des probabilités composées. propriété 1. & définition. pour tous événements $a$ et $b$ de $\omega$ tels que $p(b)\not=0$, on a : $$\boxed{\;p(a\cap b)=p b(a)\times p(b)\;}\quad (*)$$ définition 3. l’égalité (*) ci dessus s’appelle la formule des probabilités composées.
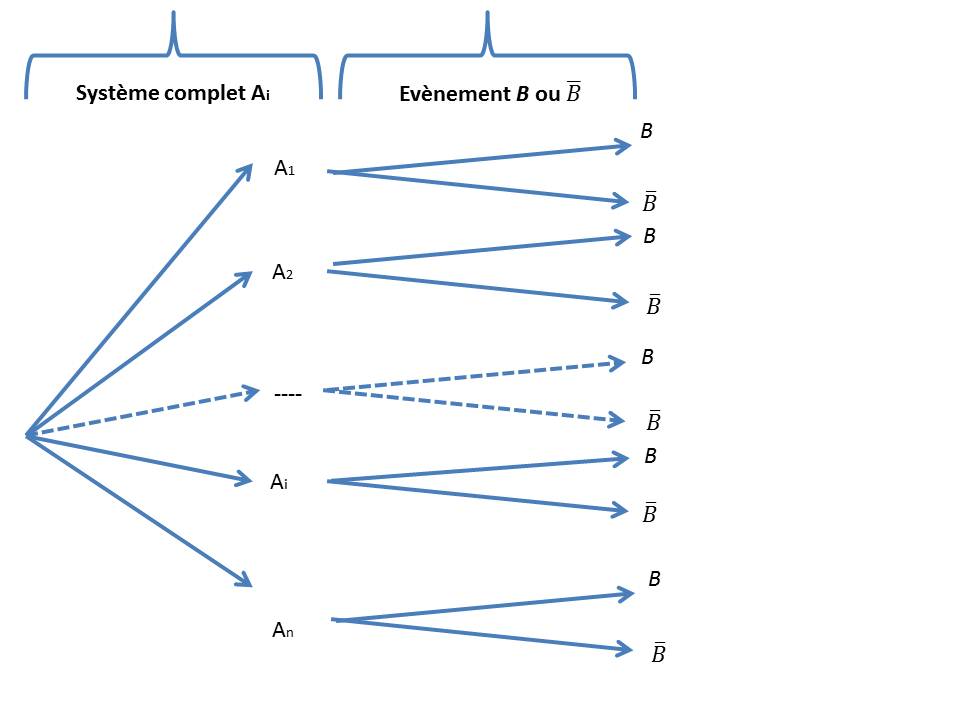
La Formule Des Probabilités Totales Preuve : formule des probabilités composées soit $\mathcal h(n)$ la proposition : « pour toute famille $(b {1},\dots,b {n})$ d'événements tels que $\mathbb p(b {1}\cap\dots\cap b {n 1})\neq0$, on a $\mathbb p(b {1}\cap\dots\cap b {n})=\mathbb p(b {1})\times\mathbb p {b {1}}(b {2})\times\dots\times\mathbb p {b {1}\cap\dots\cap b {n 1}}(b {n. 2.4. formule des probabilités composées. propriété 1. & définition. pour tous événements $a$ et $b$ de $\omega$ tels que $p(b)\not=0$, on a : $$\boxed{\;p(a\cap b)=p b(a)\times p(b)\;}\quad (*)$$ définition 3. l’égalité (*) ci dessus s’appelle la formule des probabilités composées. Théorème 6.3 : généralisation de la formule des probabilités composées. définition 6.2 : indépendance d’évènements et indépendance mutuelle. théorème 6.4 : caractérisation de l’indépendance de deux évènements. Reçois le doc pdf avec la correction : chemindelaprepa.fr exercices probabilites prepa ecg maths approfondies appliquees démonstration de la formule. Formule de probabilités composées : si \(p(a 1\cap a 2\cap\ldots\cap a n)\neq0\), alors : $${{p\left({\bigcap^n {i=1}a i}\right) }}={{p(a 1)p {a 1}(a 2)\ldots p {a 1\cap a 2\cap\ldots\cap a {n 1} }(a n) }}$$. Probabilités composées on sait que si a et b sont deux événements, a étant possible, \(p a(b)=\dfrac{p(a\cap b)}{p(a)}\) . en multipliant cette égalité par \(p(a)\) non nul, on en déduit la formule suivante :.

Document 154 Probabilite Probabilités Studocu Théorème 6.3 : généralisation de la formule des probabilités composées. définition 6.2 : indépendance d’évènements et indépendance mutuelle. théorème 6.4 : caractérisation de l’indépendance de deux évènements. Reçois le doc pdf avec la correction : chemindelaprepa.fr exercices probabilites prepa ecg maths approfondies appliquees démonstration de la formule. Formule de probabilités composées : si \(p(a 1\cap a 2\cap\ldots\cap a n)\neq0\), alors : $${{p\left({\bigcap^n {i=1}a i}\right) }}={{p(a 1)p {a 1}(a 2)\ldots p {a 1\cap a 2\cap\ldots\cap a {n 1} }(a n) }}$$. Probabilités composées on sait que si a et b sont deux événements, a étant possible, \(p a(b)=\dfrac{p(a\cap b)}{p(a)}\) . en multipliant cette égalité par \(p(a)\) non nul, on en déduit la formule suivante :.
120454 Formule de probabilités composées : si \(p(a 1\cap a 2\cap\ldots\cap a n)\neq0\), alors : $${{p\left({\bigcap^n {i=1}a i}\right) }}={{p(a 1)p {a 1}(a 2)\ldots p {a 1\cap a 2\cap\ldots\cap a {n 1} }(a n) }}$$. Probabilités composées on sait que si a et b sont deux événements, a étant possible, \(p a(b)=\dfrac{p(a\cap b)}{p(a)}\) . en multipliant cette égalité par \(p(a)\) non nul, on en déduit la formule suivante :.

Probabilités Conditionnelles Formule Des Probabilités Composées
