
Graph Theory Basics 2 Pdf Vertex Graph Theory Graph Theory Graphs are mathematical objects that are used in graph theory in order to model the relationships between objects. they are defined by 2 sets: vertices – denoted as v. these are the “elements” in our graph. edges – denoted as e. every edge connects between 2 vertices. for example, the following graph will look like this: v=\{a,b,c,d,e\}. A graph \(g\) consists of a pair \((v,e)\), where \(v\) is the set of vertices and \(e\) the set of edges. we write \(v(g)\) for the vertices of \(g\) and \(e(g)\) for the edges of \(g\) when necessary to avoid ambiguity, as when more than one graph is under discussion.

Basics In Graph Theory Pdf Vertex Graph Theory Combinatorics Graph theory is a branch of mathematics that studies the properties and applications of graphs. a graph is a collection of vertices (also called nodes) connected by edges (also called links). graphs are used to model pairwise relations between objects, making them a powerful tool for representing and analyzing complex systems in various fields. Walks, trails, paths, cycles, and circuits in a graph are sequences of vertices and edges with different properties. some allow repetition of vertices and edges, while others do not. in this article, we will explore these concepts with examples. Two vertices in a simple graph are said to be adjacent if they are joined by an edge, and an edge is said to be incident to the vertices it joins. the number of edges incident to a vertex vis called the degree of the vertex and. Graph is a collection of nodes (vertices) and connections between them (edges). if an edge e connects the vertices vi and vj, then we write e = vi, vj. an example is below. more formally, a graph is defined by a set of vertices {v1, v2, , and a set of edges } . { { v1, v2}, v1, v3}, { }.

Cycles Through Edges Pdf Vertex Graph Theory Graph Theory Two vertices in a simple graph are said to be adjacent if they are joined by an edge, and an edge is said to be incident to the vertices it joins. the number of edges incident to a vertex vis called the degree of the vertex and. Graph is a collection of nodes (vertices) and connections between them (edges). if an edge e connects the vertices vi and vj, then we write e = vi, vj. an example is below. more formally, a graph is defined by a set of vertices {v1, v2, , and a set of edges } . { { v1, v2}, v1, v3}, { }. A pseudograph g = (v,e) consists of a set v of vertices, a set e of edges, and a function g from e to {{u,v}: u,v ∈v}. an edge if a loop if f(e) = {u,u}= {u}for some u ∈v. how can we model a water pipe from a to b, and water can only flow from a to b. we use directed arrow a →b. in graph theory, we also have directed graphs. Graph representation consists of 64 vertices corresponding to the squares of the board, with an edge between vertices if there is a legal knight move between the two squares. is there a hamiltonian path (cycle) in the. Edges connect pairs of vertices. an edge can represent a physical connection between locations, like a street, or simply that a route connecting the two locations exists, like an airline flight. a loop is a special type of edge that connects a vertex to itself. loops are not used much in street network graphs. We write uv ∈ e (or u ∼ v, {u, v} ∈ e) to indicate that there is an edge between u and v in g. in this case u and v are said to be adjacent, and they are incident to th edge. for directed graphs,.

Graph Theory Pdf Vertex Graph Theory Graph Theory A pseudograph g = (v,e) consists of a set v of vertices, a set e of edges, and a function g from e to {{u,v}: u,v ∈v}. an edge if a loop if f(e) = {u,u}= {u}for some u ∈v. how can we model a water pipe from a to b, and water can only flow from a to b. we use directed arrow a →b. in graph theory, we also have directed graphs. Graph representation consists of 64 vertices corresponding to the squares of the board, with an edge between vertices if there is a legal knight move between the two squares. is there a hamiltonian path (cycle) in the. Edges connect pairs of vertices. an edge can represent a physical connection between locations, like a street, or simply that a route connecting the two locations exists, like an airline flight. a loop is a special type of edge that connects a vertex to itself. loops are not used much in street network graphs. We write uv ∈ e (or u ∼ v, {u, v} ∈ e) to indicate that there is an edge between u and v in g. in this case u and v are said to be adjacent, and they are incident to th edge. for directed graphs,.
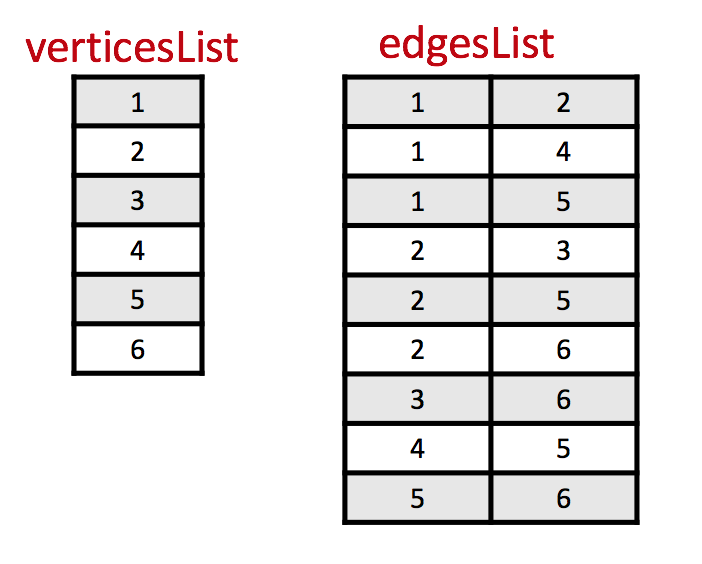
Graph Representation Edges And Vertices List Lets Code Them Up Edges connect pairs of vertices. an edge can represent a physical connection between locations, like a street, or simply that a route connecting the two locations exists, like an airline flight. a loop is a special type of edge that connects a vertex to itself. loops are not used much in street network graphs. We write uv ∈ e (or u ∼ v, {u, v} ∈ e) to indicate that there is an edge between u and v in g. in this case u and v are said to be adjacent, and they are incident to th edge. for directed graphs,.

Graph Representation Edges And Vertices List Lets Code Them Up
