
Graphing Quadratics In Vertex Form Notes Pdf Vertex Graph Theory The vertex form of a quadratic function is given by f ( x ) = a ( x h ) 2 k , where ( h, k ) is the vertex of the parabola. remember: the "vertex? is the "turning point". The vertex form of a quadratic function is f(x) = a(x h) 2 k, where (h, k) is the vertex of the parabola. the coefficient a determines whether the graph of a quadratic function will open upwards or downwards.
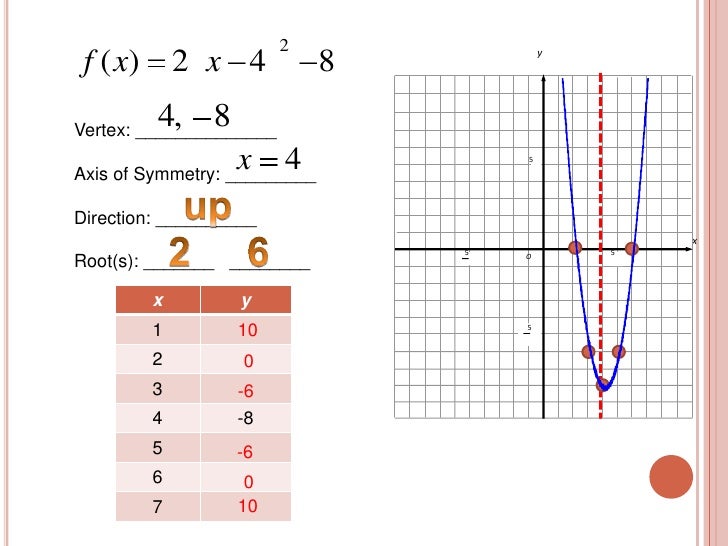
Graphing Quadratic Vertex Form The standard form or vertex form of a quadratic function is f(x) = a(x − h)2 k with real number parameters a, h, and k and a ≠ 0. notice the minus sign in front of the parameter h!! the graph of a quadratic in standard form, f(x) = a(x − h)2 k, is a graph of y = x2 that has been shifted horizontally h units and vertically k units. Explore math with our beautiful, free online graphing calculator. graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Understand how the graph of a parabola is related to its quadratic function. the vertex form of a quadratic function presents in the form [latex]f\left(x\right)=a{\left(x h\right)}^{2} k[ latex] where [latex]\left(h,\text{ }k\right)[ latex] is the vertex. how do the [latex]a[ latex], [latex]h[ latex], and [latex]k[ latex] change the parabola?. If a quadratic function is given in vertex form, it is a simple matter to sketch the parabola represented by the equation. for example, consider the quadratic function \[f(x)=(x 2)^{2} 3 \nonumber \] which is in vertex form. the graph of this equation is a parabola that opens upward. it is translated 2 units to the left and 3 units upward.

Graphing Quadratic Vertex Form Understand how the graph of a parabola is related to its quadratic function. the vertex form of a quadratic function presents in the form [latex]f\left(x\right)=a{\left(x h\right)}^{2} k[ latex] where [latex]\left(h,\text{ }k\right)[ latex] is the vertex. how do the [latex]a[ latex], [latex]h[ latex], and [latex]k[ latex] change the parabola?. If a quadratic function is given in vertex form, it is a simple matter to sketch the parabola represented by the equation. for example, consider the quadratic function \[f(x)=(x 2)^{2} 3 \nonumber \] which is in vertex form. the graph of this equation is a parabola that opens upward. it is translated 2 units to the left and 3 units upward. Quadratic functions can be written in two different forms: vertex form and intercept form. vertex form shows the vertex of the parabola, while intercept form shows the x and y intercepts of the parabola. to convert a quadratic function from standard form to vertex form, complete the square. We prefer to graph quadratic equations when it is given in vertex form f (x) = a (x – h) 2 k, where (h, k) is the vertex and h = h = − b 2 a, k = f (h). however, the quadratic equation is often represented in the standard form ax 2 bx c = 0, which first needs to be converted to the vertex using the steps shown here. Students will use vertex form to graph quadratic functions and describe the transformations from the parent function with 70% accuracy. the parent function f ( x ) = x 2 is vertically stretched by a. The lowest or highest point on the graph of a quadratic function is called the vertex. the graphs of y = x 2 and y = x 2 are symmetric about the y axis, called the axis of symmetry. in general, the axis of symmetry for the graph of a quadratic function is the vertical line through the vertex.
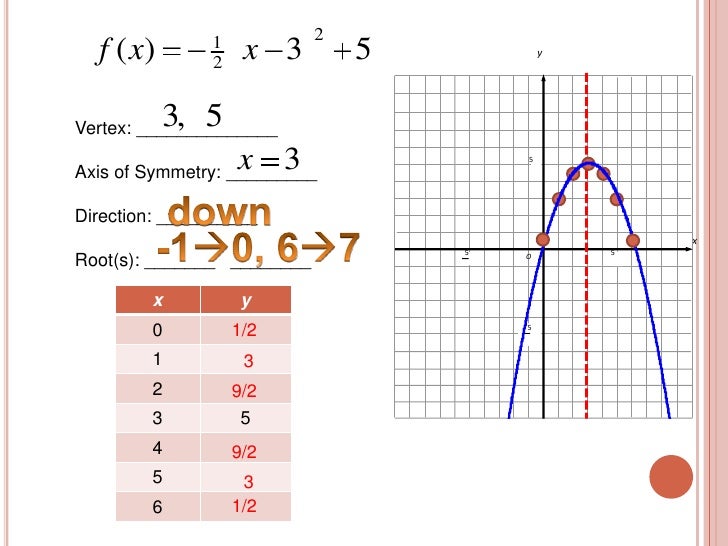
Graphing Quadratic Vertex Form Quadratic functions can be written in two different forms: vertex form and intercept form. vertex form shows the vertex of the parabola, while intercept form shows the x and y intercepts of the parabola. to convert a quadratic function from standard form to vertex form, complete the square. We prefer to graph quadratic equations when it is given in vertex form f (x) = a (x – h) 2 k, where (h, k) is the vertex and h = h = − b 2 a, k = f (h). however, the quadratic equation is often represented in the standard form ax 2 bx c = 0, which first needs to be converted to the vertex using the steps shown here. Students will use vertex form to graph quadratic functions and describe the transformations from the parent function with 70% accuracy. the parent function f ( x ) = x 2 is vertically stretched by a. The lowest or highest point on the graph of a quadratic function is called the vertex. the graphs of y = x 2 and y = x 2 are symmetric about the y axis, called the axis of symmetry. in general, the axis of symmetry for the graph of a quadratic function is the vertical line through the vertex.
