
Graphing Quadratics In Vertex Form Notes Pdf Vertex Graph Theory Show the maximum and minimum (vertex) on the graph of a quadratic function. show intercepts and the axis of symmetry on the graphs of quadratic functions. graph parabolas in different forms with and without technology. compare multiple representations of functions. To graph equations in vertex form, you will be asked to graph the vertex and two other points in order to graph the parabola. steps to graphing vertex form 1. find the vertex (h, k) and plot 2. pick a value for x other than the x of the vertex and plug it in for x to find the corresponding y and plot.
Graphing Quadratics Vertex Form Delta Learning Students will use vertex form to graph quadratic equations and describe transformations from the parent function with 70% accuracy. if a parabola opens upward, it has a lowest point. if a parabola opens downward, it has a highest point. this lowest or highest point is the vertex of the parabola. The vertex form of a quadratic function is given by f ( x ) = a ( x h ) 2 k , where ( h, k ) is the vertex of the parabola. remember: the "vertex? is the "turning point". Writing the equation in vertex form from a graph (or when given the vertex and a point) example 1: write the equation of the parabola in vertex form. identify the vertex, axis of symmetry, the maximum minimum value, and the domain and range. Graph the following quadratic functions in intercept form. label the vertex, the axis of symmetry, state the domain and range, and identify the end behavior of the graphs.
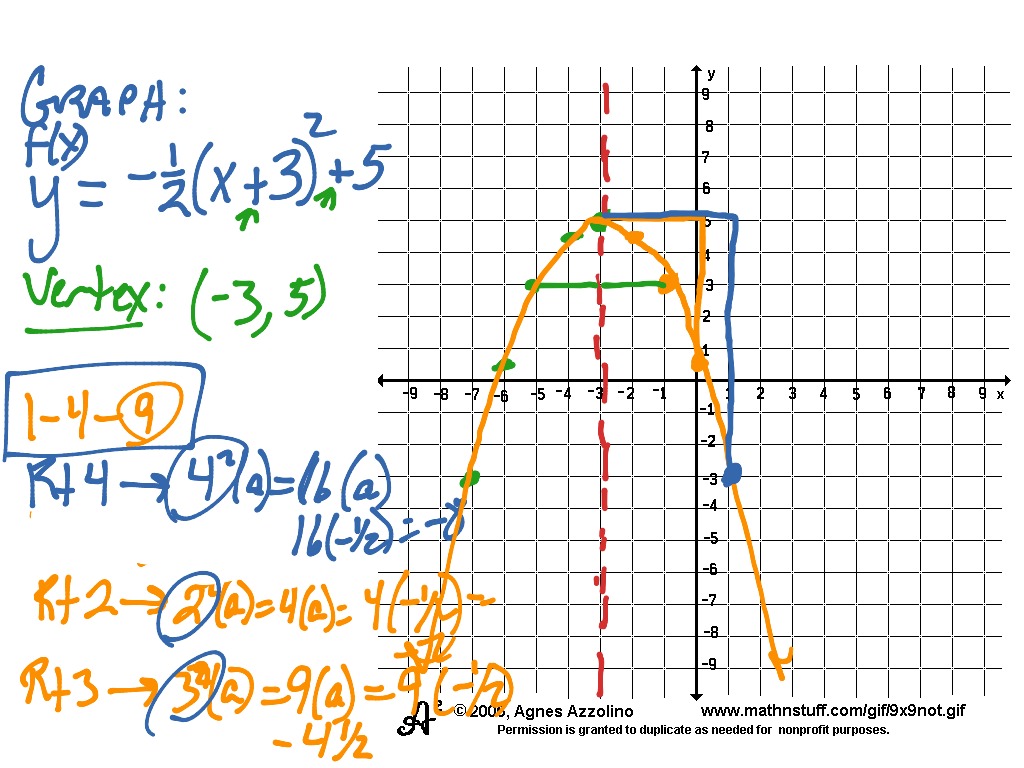
Showme 5 3 Graphing Quadratics In Vertex Form Writing the equation in vertex form from a graph (or when given the vertex and a point) example 1: write the equation of the parabola in vertex form. identify the vertex, axis of symmetry, the maximum minimum value, and the domain and range. Graph the following quadratic functions in intercept form. label the vertex, the axis of symmetry, state the domain and range, and identify the end behavior of the graphs. Understand how the graph of a parabola is related to its quadratic function. the vertex form of a quadratic function presents in the form [latex]f\left(x\right)=a{\left(x h\right)}^{2} k[ latex] where [latex]\left(h,\text{ }k\right)[ latex] is the vertex. how do the [latex]a[ latex], [latex]h[ latex], and [latex]k[ latex] change the parabola?. Section 3.3 notes page 1 . 3.3 quadratic functions . this section is all about quadratic functions, which give u shaped graphs called parabolas. first we need to define a couple of terms involving parabolas: vertex form: ( ) 2 = − y a x h k. vertex: (h, k) a > 0 opens up, vertex is a minimum . a < 0 opens down, vertex is a maximum. Recognizing that (ℎ, 𝑘) represents the vertex of the graph and use a graph to construct a quadratic equation in vertex form. students understand the relationship between the leading coefficient of a quadratic function and its concavity. 10.2 quadratics in vertex form directions: graph each function. then answer the questions. plot the vertex and at least 2 other points, more if possible. directions: compare the following function to the function in #1. describe differences and similarities. 1) b : t ; l f2 : t e1 ; 69 standard form:.
