How Many 5 Digit Numbers Divisible By 5 Can Be Formed From 0 1 3 4 5 7 9 Repetition Allowed

Questionnhow Many Four Digit Numbers Divisible By 5 Can Be Formed How many 5 digit numbers divisible by 5 can be formed from 0, 1, 3, 4, 5, 7, 9. repetition allowed. no description has been added to this video. Recognize that the problem involves selecting 5 digits from the set of digits 0, 1, 3, , 9 to form a 5 digit number that is divisible by 5. since repetition is allowed, the first digit cannot be 0.

Solved 1 How Many Three Digit Numbers Divisible By 15 Can Be Formed Find the number of 5 digit numbers divisible by 5 that can be formed using the digits 0,1,2,3,4,5 when repetition is allowed. solution in telugu. the correct answer is: =2×5×6×6×6= 2160 ways. I can do the case when repetition is not allowed, where we can remove either $0$ or $3$ and work with the rest of the digits (as the sum of the digits is divisible by $3$). The first digit (from left) cannot be 0, so we have 4 ways to chose it. the second digit from the left can have the value 0, and we'll not repeat the number at the first digit again, so we have 3 ways to chose this number. Without digit repetition, each digit can only be chosen once, which reduces the number of choices for each position. by analyzing the patterns of 5 digit numbers meeting the criteria, we can see that there are a total of 1680 possible arrangements. learn more about permutations here: brainly question 23283166 #spj11.

Solved 9 How Many 3 Digit Numbers That Are Divisible By 5 Chegg The first digit (from left) cannot be 0, so we have 4 ways to chose it. the second digit from the left can have the value 0, and we'll not repeat the number at the first digit again, so we have 3 ways to chose this number. Without digit repetition, each digit can only be chosen once, which reduces the number of choices for each position. by analyzing the patterns of 5 digit numbers meeting the criteria, we can see that there are a total of 1680 possible arrangements. learn more about permutations here: brainly question 23283166 #spj11. If 0 is the first digit, then number of places left to be filled is 4 and that can be done in 4! ways. so, the 5 digits numbers that can be formed which ends with is 120 4! = 96. How many four digit numbers divisible by 5 can be formed using the digits 0, 1, 3, 5, 7, 9 if repetition is not allowed and the digits 0 and 1 are not allowed to be placed next to each other?note t. To find the number of four digit numbers divisible by 5 that can be formed using the given digits without repetition and with the constraint of not placing 0 and 1 next to each other, we can use a step by step approach. The two divisiblity rules you are assumed to use are: divisible by $5$ if and only if last digit is $0$ or $5$ and; divisible by $3$ if and only if the sum of the digits add to a multiple of $3$.

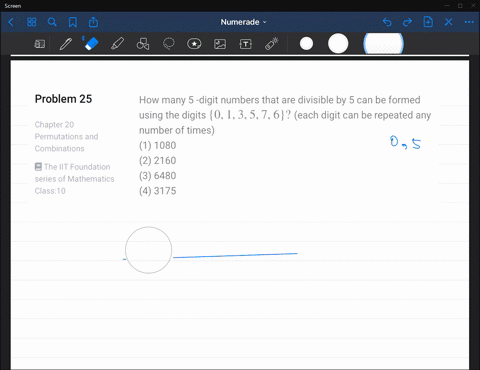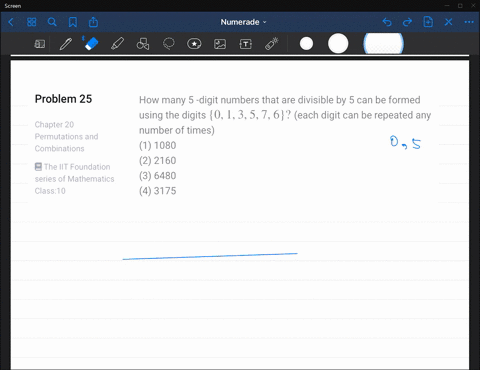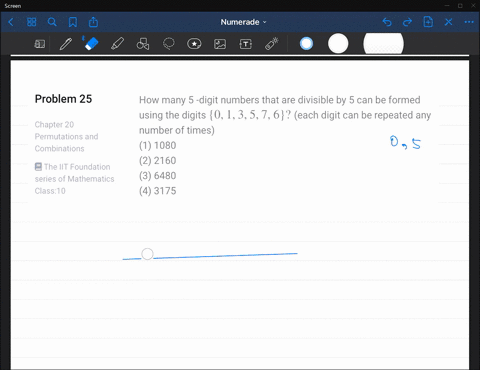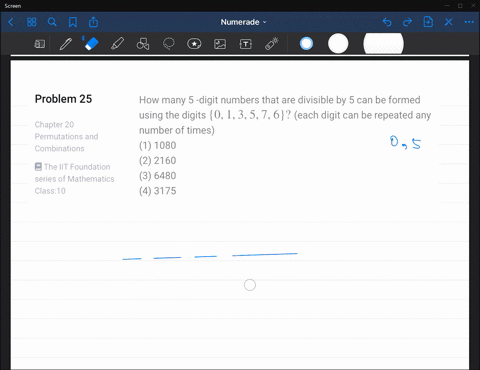
Solved How Many 5 Digit Numbers That Are Divisible By 5 Can Be Formed If 0 is the first digit, then number of places left to be filled is 4 and that can be done in 4! ways. so, the 5 digits numbers that can be formed which ends with is 120 4! = 96. How many four digit numbers divisible by 5 can be formed using the digits 0, 1, 3, 5, 7, 9 if repetition is not allowed and the digits 0 and 1 are not allowed to be placed next to each other?note t. To find the number of four digit numbers divisible by 5 that can be formed using the given digits without repetition and with the constraint of not placing 0 and 1 next to each other, we can use a step by step approach. The two divisiblity rules you are assumed to use are: divisible by $5$ if and only if last digit is $0$ or $5$ and; divisible by $3$ if and only if the sum of the digits add to a multiple of $3$.

How Many Six Digit Numbers Can Be Formed From The Digits 1 2 3 4 5 6 To find the number of four digit numbers divisible by 5 that can be formed using the given digits without repetition and with the constraint of not placing 0 and 1 next to each other, we can use a step by step approach. The two divisiblity rules you are assumed to use are: divisible by $5$ if and only if last digit is $0$ or $5$ and; divisible by $3$ if and only if the sum of the digits add to a multiple of $3$.

24 How Many Five Digit Numbers Divisible By 6 Can Be Formed By Using