
How To Solve An Exponential Equation Mathsathome It can be used in enumeration trees, combinatorics, maxima of planck, bose einstein, and fermi dirac distribution, in enzyme kinetic in biochemistry, and in machine learning algorithms. learn more. This article shows a few examples of using sas and the lambert w function to solve implicit equations in which the variable (x) occurs as an exponent and also in a linear term. for each equation, you can convert it into a standard form and apply the lambert w function.
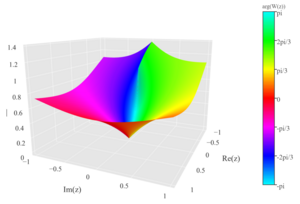
Lambert W Function Wikiwand Lambert’s w function. if you can solve one equation involving exponential functions you can bootstrap your solution solve a lot more equations. the lambert w function is defined to be the function w(x) that maps each x to a solution of the equation. w exp(w) = x. this function is implemented python under scipy.special.lambertw. let’s see. Solving equations with the lambert w functionfor more info on the lambert w function:introduction video: youtu.be puha etbwj8playlist: . In this video we use the lambert w function to find the general solution of the exponential equation a^x bx c=0. more. As an alternative to using the lambert w function, you can solve it numerically, for example with the newton raphson method. to apply the lambert w function, multiply both sides by x ln(2) x ln (2) to get. ln(2) = x ln(2)2x ln (2) = x ln (2) 2 x. since 2x = ex ln(2) 2 x = e x ln (2), ln(2) = x ln(2)ex ln(2) ln (2) = x ln (2) e x ln (2).

Lambert W Function From Wolfram Mathworld In this video we use the lambert w function to find the general solution of the exponential equation a^x bx c=0. more. As an alternative to using the lambert w function, you can solve it numerically, for example with the newton raphson method. to apply the lambert w function, multiply both sides by x ln(2) x ln (2) to get. ln(2) = x ln(2)2x ln (2) = x ln (2) 2 x. since 2x = ex ln(2) 2 x = e x ln (2), ln(2) = x ln(2)ex ln(2) ln (2) = x ln (2) e x ln (2). There are two ways to do this: in some very special cases, one can extract out of w(·) if the dot is one of a few numbers like those we saw above: 0, 1, e, etc, in which case the expression is replaced by a number of some sort. w0(xx 1 ln x) = x ln x . This lesson explains how to solve an equation with 2 variables; one as the base and the other as an exponent.you will learn about the lambert w function, whi. To answer your question yes, you can, pretty much the same way you solve any system of equations try to reduce to one equation in one unknown, then use the w function is appropriate. how you reduce, of course, depends on the equations themselves. Rewrite the equation using the exponential function $e^x$: \[ e^{x \ln 2} = 5 x. \] next bring the equation to the form $y = x e^x$ where $y$ will be a specific number. then we can use the lambert functions to solve this equation.

Solved Problem Iii 25 Points Apply The Lambert W Function Chegg There are two ways to do this: in some very special cases, one can extract out of w(·) if the dot is one of a few numbers like those we saw above: 0, 1, e, etc, in which case the expression is replaced by a number of some sort. w0(xx 1 ln x) = x ln x . This lesson explains how to solve an equation with 2 variables; one as the base and the other as an exponent.you will learn about the lambert w function, whi. To answer your question yes, you can, pretty much the same way you solve any system of equations try to reduce to one equation in one unknown, then use the w function is appropriate. how you reduce, of course, depends on the equations themselves. Rewrite the equation using the exponential function $e^x$: \[ e^{x \ln 2} = 5 x. \] next bring the equation to the form $y = x e^x$ where $y$ will be a specific number. then we can use the lambert functions to solve this equation.

Lambert W Function From Wolfram Mathworld To answer your question yes, you can, pretty much the same way you solve any system of equations try to reduce to one equation in one unknown, then use the w function is appropriate. how you reduce, of course, depends on the equations themselves. Rewrite the equation using the exponential function $e^x$: \[ e^{x \ln 2} = 5 x. \] next bring the equation to the form $y = x e^x$ where $y$ will be a specific number. then we can use the lambert functions to solve this equation.
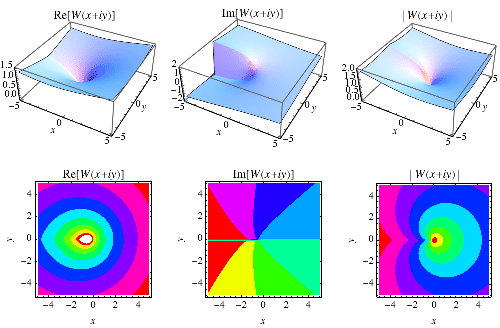
Lambert W Function From Wolfram Mathworld
